Material Dourado: como usar?

Descubra como usar o Material Dourado, a partir de um passo a passo detalhado e várias dicas de atividades.

Olá! Que bom ter você aqui!

O Material Dourado é um recurso incrível para ajudar na compreensão do nosso sistema de numeração.

Nos anos iniciais, é muito importante trabalhar com materiais concretos, pois eles permitem que estudantes experimentem, manipulem e visualizem ideias matemáticas de forma tangível.

Grande parte das dificuldades de aprendizagem na matemática está em compreender os conceitos abstratos. Por isso, é muito eficaz utilizar recursos manipuláveis como o Material Dourado, para apresentar um conceito.

Depois que os alunos compreenderem, criando uma base sólida, gradualmente, inserimos representações mais simbólicas e abstratas.

Porém, muitos de nós, não aprendemos a refletir sobre a matemática, mas sim resolver atividades de forma mecânica.

Diante disso, é difícil saber como usar o Material Dourado, explorando as diversas possibilidades. 

Depois que aprendi a usar esse material fiquei encantada com a riqueza dele e utilidade para ajudar os alunos, principalmente aqueles que têm dificuldades de aprendizagem em matemática.

Por isso, resolvi fazer este post para ajudar você, professor ou professora, a entender como funciona o Material Dourado. 

Vou apresentar o passo a passo, explicadinho, mostrando como utilizar o MD para trabalhar composição, decomposição, resolver adição, subtração, multiplicação e divisão. Além de apresentar várias dicas de atividades e estratégias.

Acompanhe o post e pratique!

O que é Material Dourado?

O Material Dourado foi criado pela médica e educadora italiana Maria Montessori (1870-1952).

Maria Montessori acreditava na educação sensorial e na importância da prática para o aprendizado. Ela criou o material para facilitar a compreensão de conceitos matemáticos.

Mas, por que dourado se os materiais que vemos são de madeira ou E.V.A colorido? Porque o material original era construído com contas douradas, daí a origem do nome.

Esse é um recurso muito útil nas escolas, pois serve para representar nosso sistema de numeração decimal.

Geralmente, é feito de madeira e encontrado em papelarias. Mas, se você não tiver acesso ao material pronto, você pode desenhar os quadradinhos no E.V.A e recortar. Outra possibilidade é imprimir e plastificar.

Como funciona o Material Dourado?

O Material Dourado (MD) é constituído de cubinho, barra, placa e cubo.

Funciona assim:

• O cubinho representa a unidade.
• A barra representa a dezena, ou seja, 10 unidades. Como podemos observar, a barra é formada por 10 cubinhos agrupados.
• A placa representa a centena ou 10 dezenas, ou ainda 100 unidades.

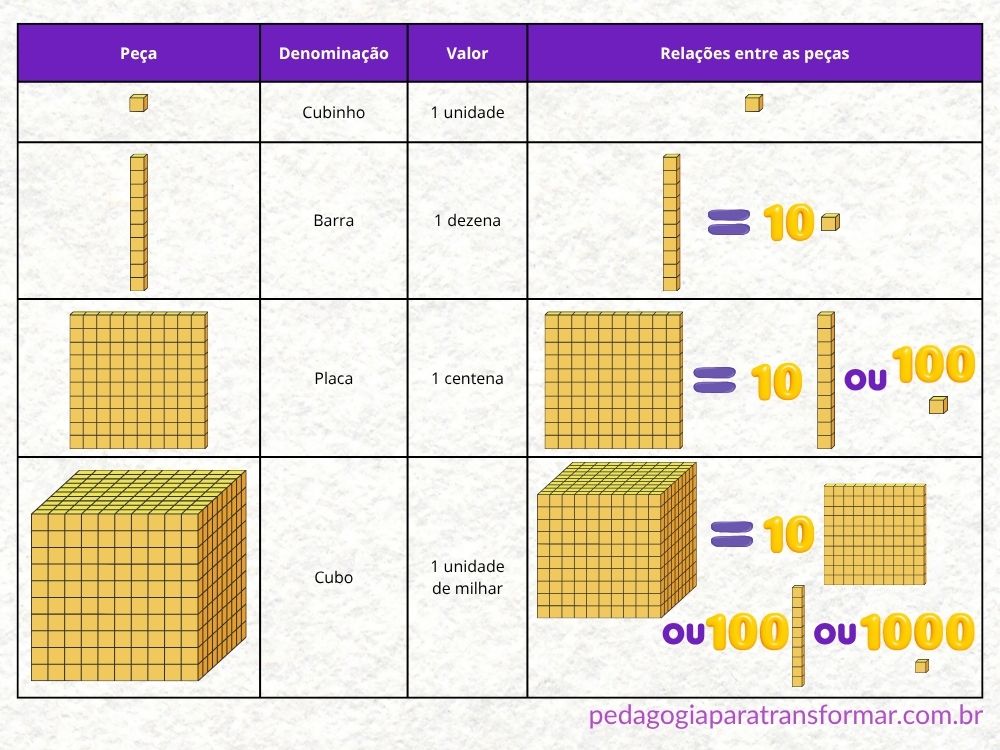
Como podemos observar, na placa temos 100 cubinhos agrupados. Mas, também podemos dizer que são 10 barras agrupadas.

• O cubo representa a unidade de milhar. São 10 centenas, ou 100 dezenas ou ainda, 1000 unidades.

Como podemos observar, o cubo é formado com 10 placas juntinhas. Ou 100 barras agrupadas. Ou 1000 cubinhos.

Isso significa que no cubo não podemos contar somente as 6 faces. Mas, entender como 10 placas justapostas.

Por que o Material Dourado é importante para compreensão do Sistema de Numeração Decimal?

1. Ele facilita o entendimento da base 10 do nosso SND

Isso porque as trocas se dão de 10 em 10:

• 10 cubinhos (unidades) são trocados por 1 barra (dezena).
• 10 barras (dezenas) são trocadas por 1 placa (centena).
• 10 placas (centenas) são trocadas por 1 cubo (unidade de milhar).

2. Ele facilita a compreensão do sistema aditivo

Para representar determinado numeral, é só somar os valores individuais de cada peça.

Dessa forma, é possível realizar diversas atividades com o MD para ajudar as crianças a compreenderem o Sistema de Numeração Decimal. Pois esse conhecimento será muito útil para que compreendam, posteriormente, os significados e procedimentos das operações numéricas.

Quais são as limitações do Material Dourado?

O Material Dourado, por si só, não possibilita a compreensão do sistema posicional.

O que significa que não é exigido que as peças sejam colocadas em uma ordem, como acontece no nosso SND.

Por exemplo, para representar o número 145 podemos usar as peças de diversos modos. Para ler o número escrito, basta somar os valores individuais de cada peça, independentemente da posição que ela está.

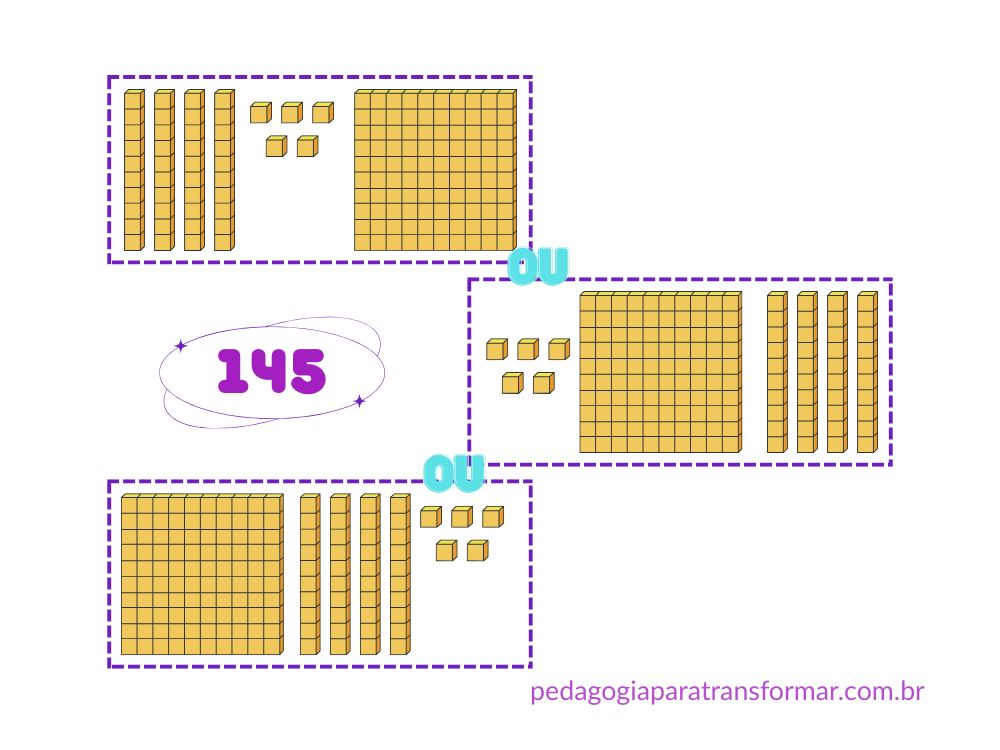
Outras limitações do material é que ele não é um sistema multiplicativo e por não ser posicional, não representa o zero.

Como superar essas limitações do MD?

Uma possibilidade que gosto de utilizar é fazer o quadro valor de lugar como se fosse um “tapetinho” de E.V.A. Assim, os alunos precisam colocar as peças na “casinha” correta.

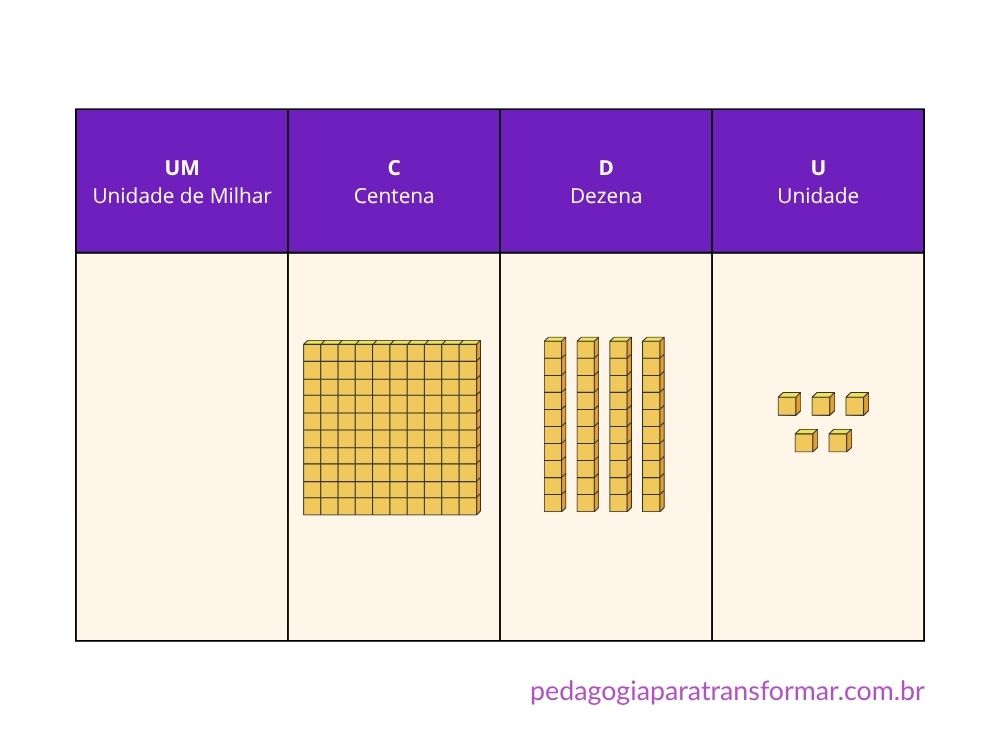
Como usar o Material Dourado para ensinar composição e decomposição?

Quando os alunos ainda não têm familiaridade com o MD, deixe que explorem de forma lúdica, em grupos.

Em seguida, apresente as peças e como são nomeadas. Você pode fazer um cartaz e ir preenchendo-o enquanto apresenta o material e faz alguns questionamentos aos alunos.

Exemplos de questionamentos e reflexões que você pode usar para ajudar os alunos a compreender decomposição e composição de números utilizando o Material Dourado:

• Quantos cubinhos preciso juntar para formar uma barra?
• Quantas barras preciso juntar para formar uma placa?
• Quantas placas preciso juntar para formar um cubo?
• Se trocarmos 10 unidades por 1 dezena, o número muda? Por quê?
• Se tirarmos 1 dezena do número 87, quando sobra? Como fica no material?
• Você consegue montar o número 132 utilizando o Material Dourado? Depois, explique para os colegas como fez.
• Eu tenho 2 placas, 3 barras e 5 cubinhos. Que número está representado?
• Represente o número 156 com centenas, dezenas e unidades. E se usarmos só dezenas e unidades, como seria?
• Quantas dezenas existe no número 140? Monte o número somente com barras.
• Se eu disser que um número tem 3 centenas, 5 dezenas e nenhuma unidade, qual é o número? Represente com o Material Dourado.

Como usar o Material Dourado para ensinar adição?

Convido você para calcularmos algumas operações, passo a passo. Vamos lá?

Primeiramente, vamos calcular 23+35.

Ana tinha 35 livros em sua estante. Em seu aniversário, ela ganhou 23 livros para completar sua coleção. Quantos livros Ana tem agora em sua estante?

1. Vamos representar cada um dos numerais. 
2. Depois, é só juntar as peças e ler o resultado. Ou seja, 5 barras (50) e 8 cubinhos (8) = 58

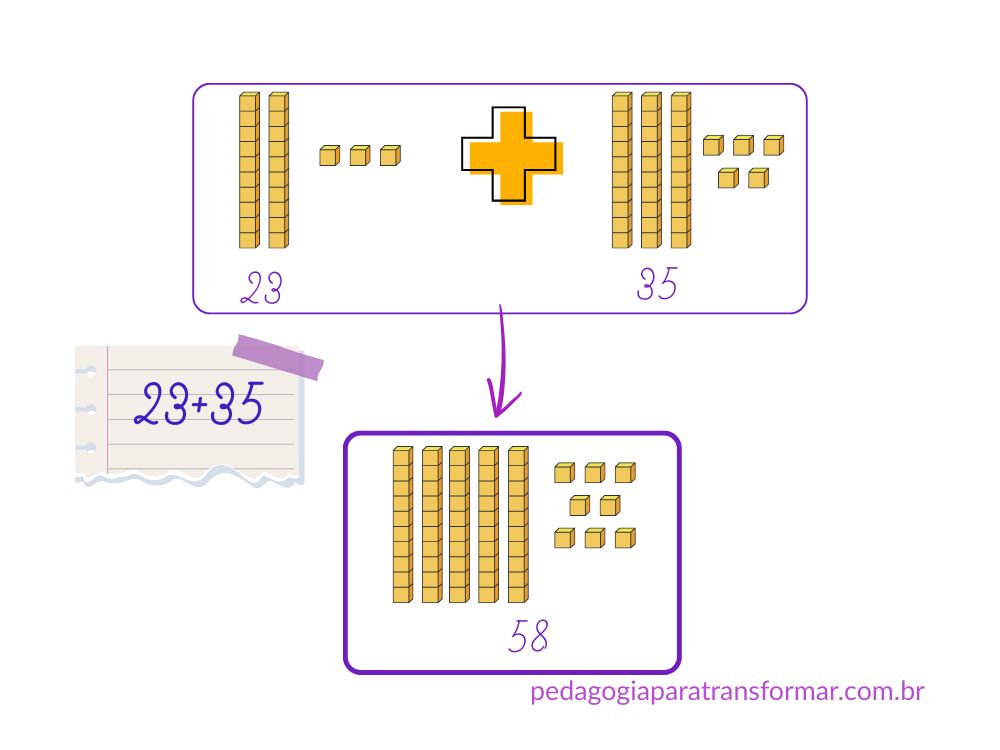
Nesse exemplo, nenhuma troca precisou ser efetuada.

Agora, vamos calcular uma adição com reagrupamento ou reserva: 29+35.

Em uma festa de aniversário, havia 29 adultos e 35 crianças. Quantas pessoas havia na festa?

1. Vamos representar cada um dos numerais. Depois, vamos juntar as peças. Ficamos com 5 barras e 14 cubinhos.
2. Porém, como aprendemos na base 10, quando temos 10 unidades, devemos agrupá-las. Pois, a regra é nunca 10!
3. Sendo assim, vamos juntar esses 10 cubinhos e trocar por uma barrinha. Então, agora, temos 6 barrinhas (60) e 4 cubinhos (4) que sobraram. Portanto, 64.

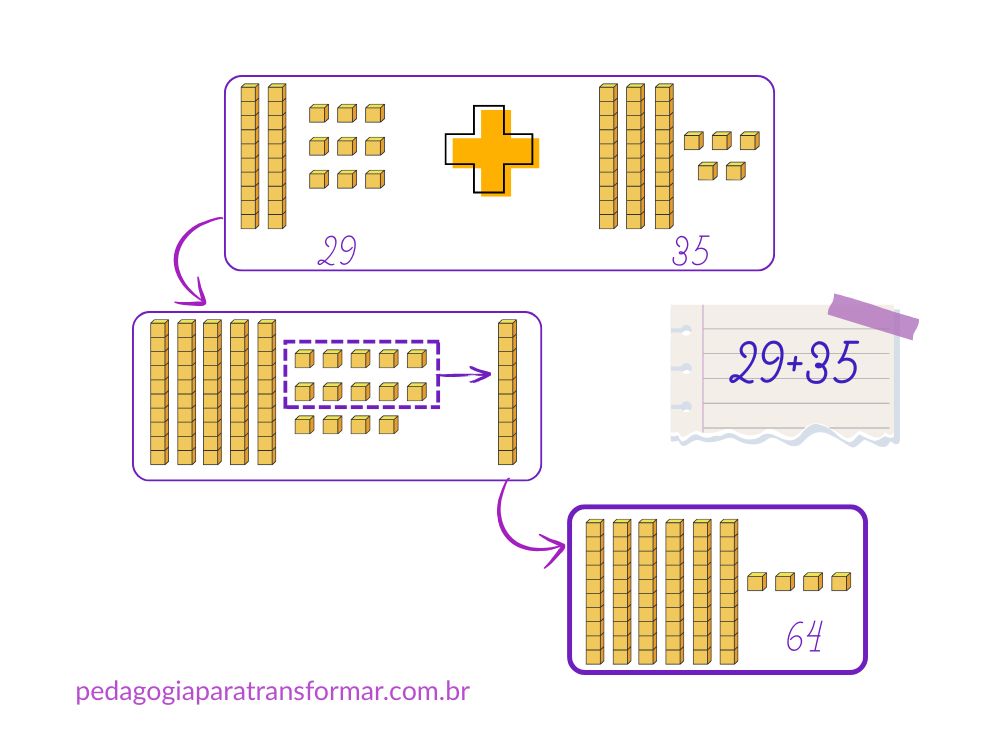
Essa é uma maneira muito lúdica e eficaz de entender o que chamamos de “vai um” (erroneamente). Muitas vezes, as crianças não entendem o porquê desse processo.

Com o Material Dourado, elas podem compreender que na verdade o 1 “surgiu” porque 10 unidades foram agrupadas em 1 dezena.

Como usar o Material Dourado para ensinar subtração?

Subtração com o sentido de retirar

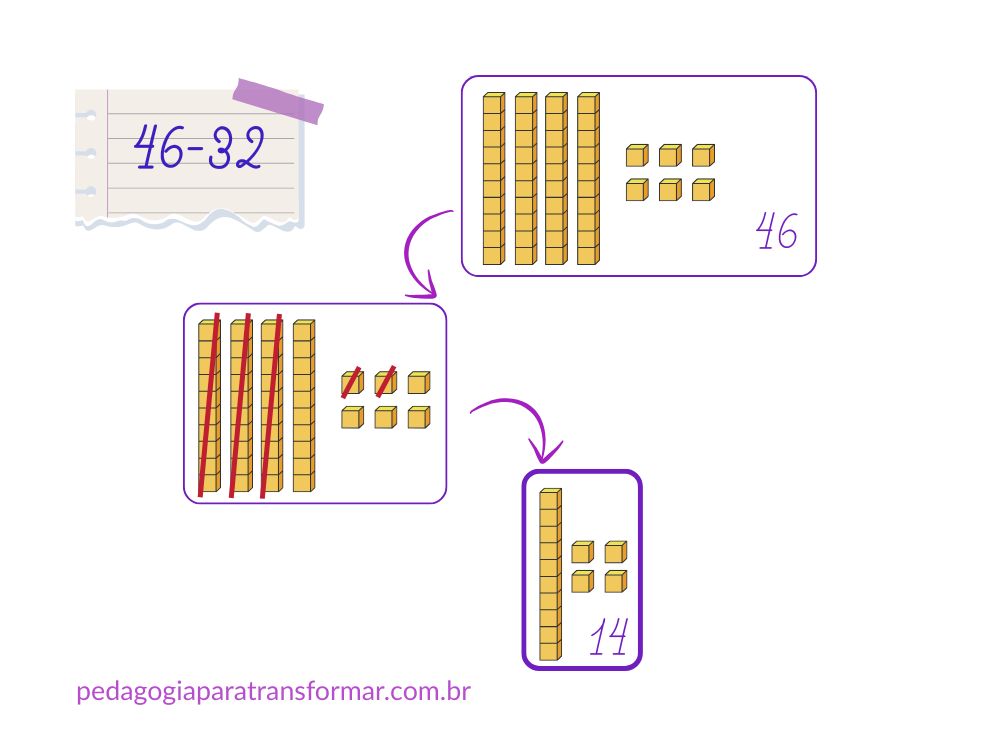
Joana tem 46 figurinhas repetidas em sua coleção. Ela decidiu dar 32 figurinhas para uma amiga que está começando sua própria coleção. Quantas figurinhas repetidas ficaram com Joana depois de presentear a amiga?

1. Inicialmente, vamos representar a quantidade maior (46) com as peças do Material Dourado. Pois, na subtração com MD podemos representar somente o 46 e retirar 32.
2. Em seguida, retiramos 3 barras e 2 cubinhos.
3. Sobraram 1 barra e 4 cubinhos, portanto, 14.

Agora, vamos resolver um exemplo de subtração com reagrupamento ou com reserva.

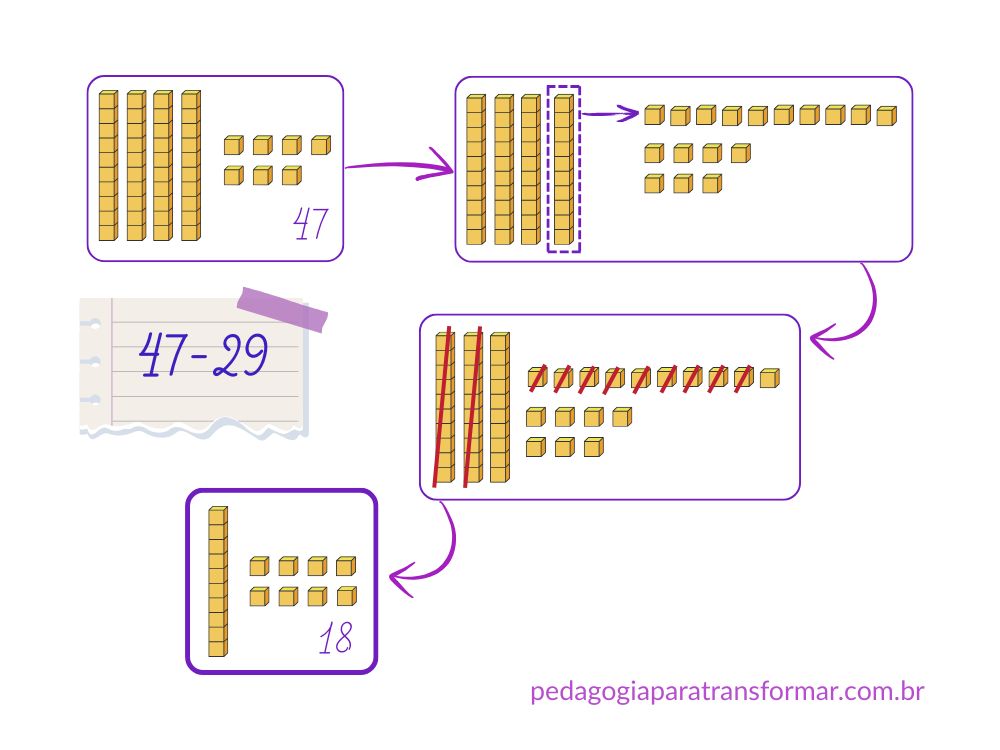
Miguel está juntando dinheiro para comprar um joguinho que custa 47 reais. Ao abrir seu cofrinho constatou que já tem 29 reais. Quantos reais faltam para ele conseguir comprar o jogo?

1. Aqui também vamos representar 47 com o Material Dourado e retirar 29.
2. Mas, como vamos retirar 9 cubinhos se há apenas 7?
3. Precisamos trocar uma barrinha por 10 cubinhos (uma dezena por 10 unidades). O que tradicionalmente, nomeamos (erroneamente) como “pegar emprestado”. Então, o número 47 passa a ser representado assim: 3 barras e 17 cubinhos.
4. Agora é possível retirar 29 (2 barras e 9 cubinhos).
5. Restaram 1 barra e 8 cubinhos, portanto, 18.

Subtração com o sentido de comparar

Imagine o seguinte problema:

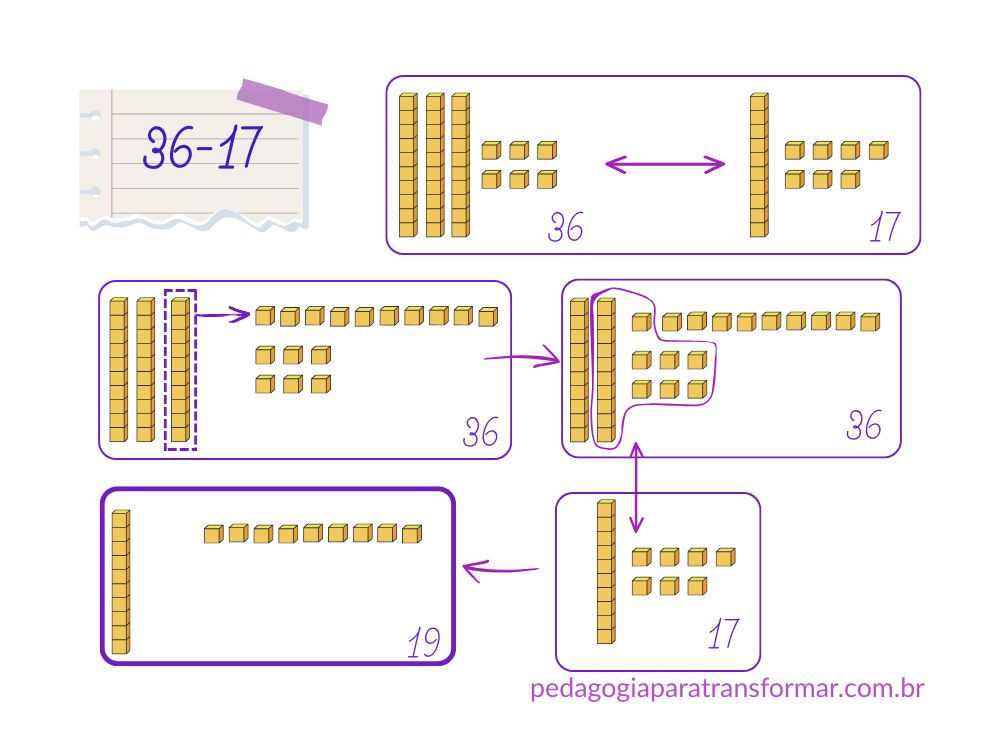
Camila tem 36 lápis de cor. Jéssica tem 17. Quantos lápis Camila tem a mais que Jéssica?

1. Uma vez que esse problema tem o sentido de comparar, podemos representar as duas quantidades.
2. Não é possível encontrar a quantidade 17 na representação de 36. Por isso, vamos trocar 1 dezena por 10 unidades.
3. Agora, ficou fácil comparar. Camila tem 19 lápis a mais que Jéssica.

Situação de completar

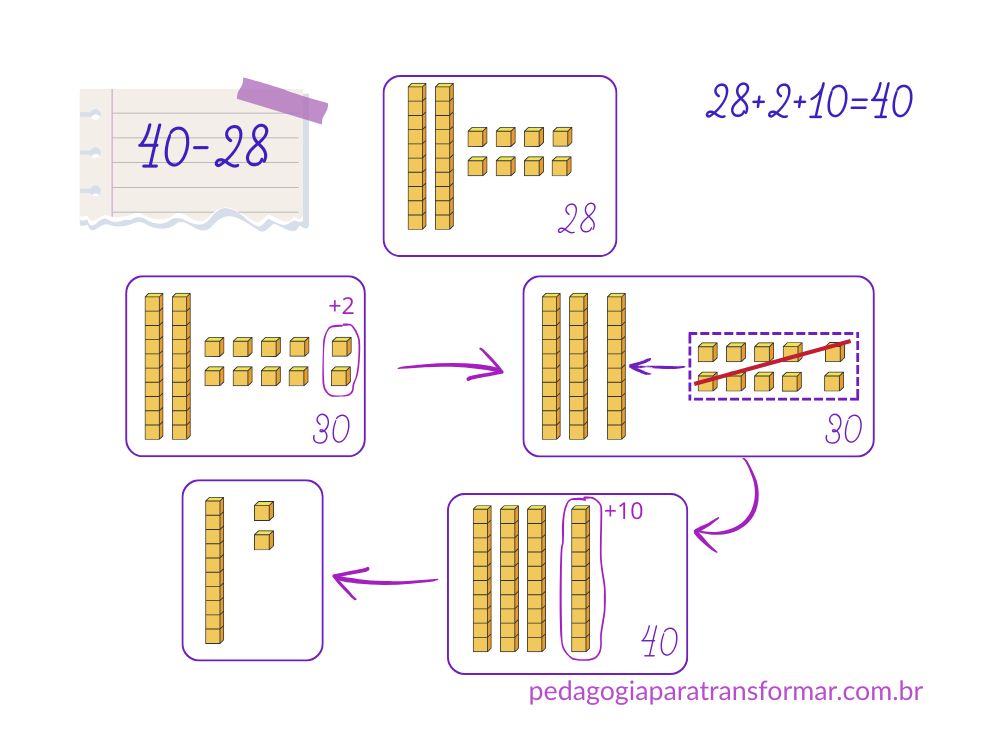
João tem um álbum de 40 figurinhas. Ele já tem 28 figurinhas. Quantas figurinhas faltam para completar o álbum?

Nesse caso, temos que completar. Se ele tem 28 figurinhas, quantas faltam para chegar a 40?

1. Adicionamos 2 unidades e assim, chegamos ao número 30.
2. Adicionamos 1 dezena e assim, chegamos ao número 40.
3. Portanto, complementamos 2 unidades + 1 dezena = 12

Como usar o Material Dourado para ensinar multiplicação?

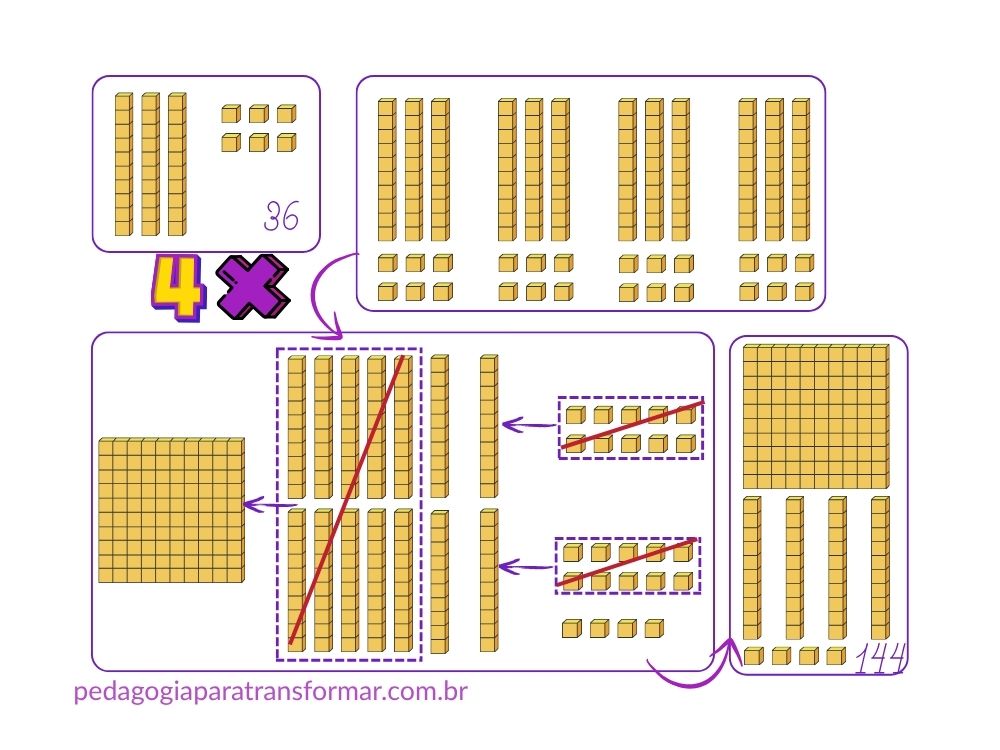
Vamos resolver a seguinte situação-problema: Heitor comprou 4 cadernos. Cada um custou 36 reais. Quantos reais ele gastou para comprar os cadernos?

1. Se cada caderno custa 36 reais, vamos representar 36 com o Material Dourado. 
2. Se são 4 cadernos, em seguida, vamos multiplicar por 4, tanto as unidades (cubinhos), quanto as dezenas (barras). Ou seja, representar o número 36 quatro vezes.
3. Posteriormente, é preciso realizar as trocas, pois não podemos ter 10 peças iguais.

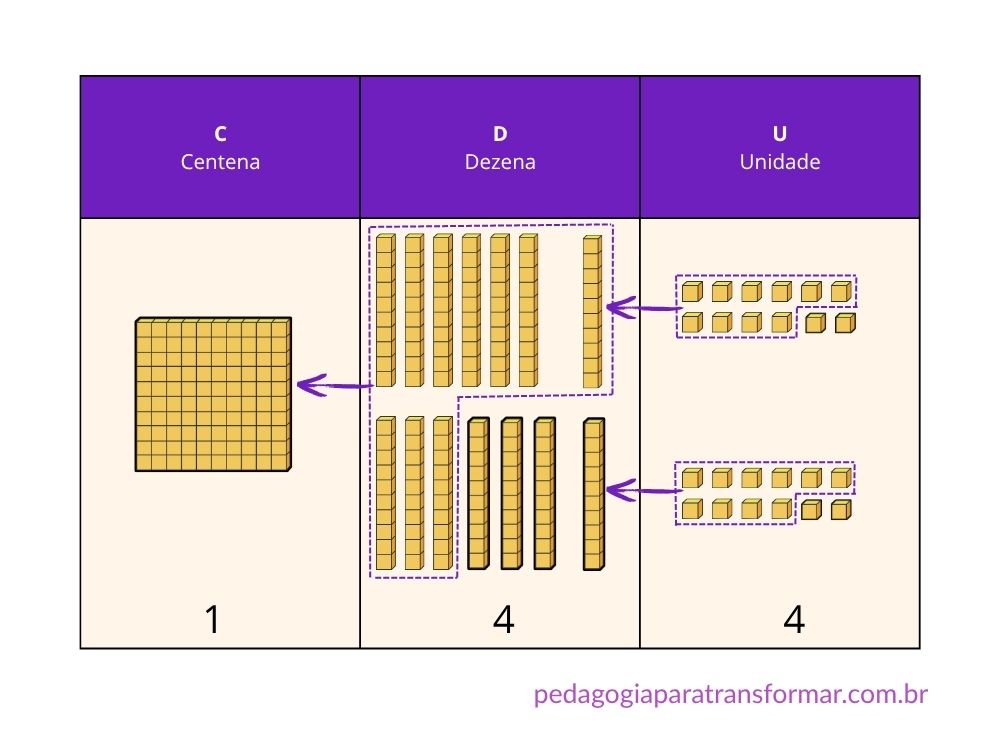
Utilizando o Q.V.L ficaria assim:

Como usar o Material Dourado para ensinar divisão?

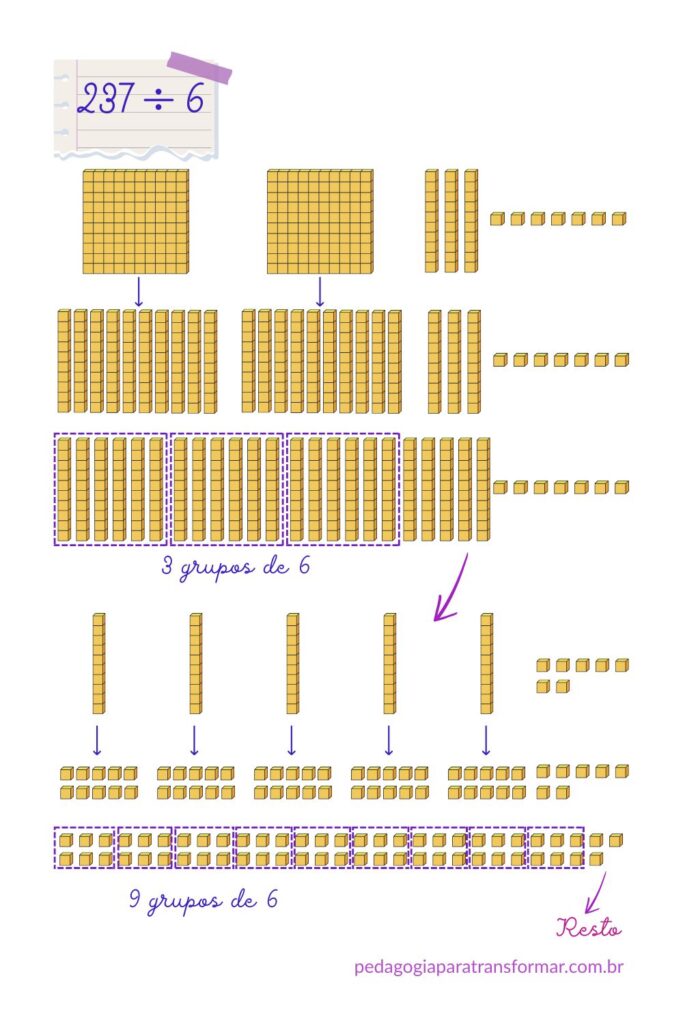
Paola trabalha em uma gráfica e recebeu um pedido de impressão de 237 panfletos para uma campanha publicitária. Ela precisa organizar os panfletos em pacotes com exatamente 6 unidades cada. Quantos pacotes completos ela conseguirá formar e quantos panfletos, se houver, irão sobrar?

1. Representamos 237 com o Material Dourado.
2. Para dividir 2 placas (centenas) por 6, temos que efetuar a troca das 2 placas por 10 barras (dezenas) cada uma delas. Assim, ficamos com 23 barras, certo?
3. Como temos 23 barras, agora é possível formar grupos de 6. Observe que foi possível formar 3 grupos de 6 barras e sobraram 5. Isso significa que o quociente parcial é 3 dezenas ou 30.
4. Como restaram 5 dezenas e 7 unidades, podemos continuar dividindo, já que 57 é maior que 6.
5. Mas, aqui temos outro problema. Como vou dividir 5 barras por 6? Precisamos efetuar a troca de 5 barras por 10 cubinhos, cada uma delas.
6. Agora, temos 57 cubinhos, ou seja, 57 unidades. Sendo assim, agora é possível formar grupos de 6 cubinhos.
7. Formamos 9 grupos de 6 e sobraram 3 cubinhos. Como não é possível dividir mais, já que 3 é menor que 6, o resto dessa divisão é 3.

Outras possibilidades de uso do Material Dourado

• Realize um jogo de dados, no qual todos os jogadores começam com 9 pontos, representados por 9 cubinhos. Ao ganhar mais pontos, devem trocá-los por uma barra, e assim por diante.
• Sorteie números para que os alunos possam representá-los com Material Dourado. Você pode realizar uma gincana entre grupos.
• Desafie os alunos a decompor um número de maneiras diferentes. Ex.: 52 pode ser 5 barras + 2 cubinhos, ou 4 barras + 12 cubinhos, ou 52 cubinhos.
• Proponha a construção de uma sequência numérica (ex: 100, 110, 120…) com o MD, e incentive os alunos a observar o que muda em cada passo. Assim, eles podem visualizar as regularidades.
• Convide dois alunos para montar números diferentes (pode ser definido por sorteio) com o MD e peça que comparem: “Quem tem mais?” “Qual é a diferença?”
• Realize atividades impressas de sistematização sobre o que foi trabalhado com o material concreto, para reforçar a aprendizagem. Você pode realizar atividades lúdicas também nessa proposta, como bingo e jogos variados.

Conclusão

São muitas possibilidades para usar o Material Dourado em sala de aula. Esse é um material muito rico e facilita muito a compreensão dos conceitos matemáticos, principalmente para os alunos com dificuldade de aprendizagem.

Agora você está animada(o) para usar o Material Dourado em suas aulas?