Como ensinar tabuada para crianças de forma simples, com compreensão

Descubra como ensinar tabuada para crianças, prezando a compreensão e só depois, a memorização. Neste post, você encontra várias ideias e reflexões interessantes para colocar em prática com seus alunos!

Olá! Que bom ter você aqui!

Ensinar a tabuada de multiplicação para crianças não precisa ser algo chato. E é bom que não seja.

Pois a maneira como ensinamos nos anos iniciais do ensino fundamental terá muita influência em como os estudantes lidarão com a tabuada durante a vida escolar.

Entretanto, não é fácil para os professores. Pois a própria sociedade traz uma imagem ruim da tabuada, como algo difícil, que deve ser decorada e repetida sem errar.

Alguns alunos conseguem memorizar rapidamente, mas sabemos que nem todos conseguem. Assim, alguns estudantes, mesmo estando em séries avançadas, apresentam muita dificuldade na multiplicação.

Por isso, temos que buscar estratégias e, muitas vezes, retomar uma compreensão da tabuada que não foi consolidada em anos anteriores.

Uma vez que quando é trabalhada somente a memorização, as crianças não conseguem mobilizar conhecimentos para resolver problemas quando a memória falha.

Se você está em busca de metodologias para ensinar a tabuada para crianças, com compreensão, neste post você vai encontrar muitas ideias. Boa leitura!

Para início de conversa

A tabuada costuma ser temida por muitos estudantes, chegando a gerar ansiedade. Principalmente, para alunos que têm dificuldade de aprendizagem na matemática.

Uma das primeiras coisas que devemos refletir é que a tabuada não é pré-requisito para a multiplicação. 

Isso significa que primeiro devemos trabalhar problemas reais envolvendo a multiplicação.

Depois, quando os alunos tiverem compreendido o conceito, a tabuada vai fazer sentido para eles, como um cálculo que vai facilitar a resolução.

Atualmente, muitos alunos não conseguem resolver problemas de multiplicação e divisão porque não memorizaram a tabuada. É muito importante memorizar, pois facilita a resolução de problemas.

Mas, será que não saber a tabuada de cor é um impedimento para resolver um problema de multiplicação? Não existem outras maneiras?

Vamos supor que um aluno repetiu a tabuada várias vezes, decorou tudo. Na hora da prova, ele ficou muito nervoso e esqueceu quanto é 9×8. Ele não consegue lembrar de jeito nenhum.

Só que ele sabe de cor que 9×10 é igual a 90. Mas, como ele decorou a tabuada como se fosse uma lista de números que alguém inventou do nada, ele não consegue pensar em outras estratégias.

Para ele, saber quanto é 9×10 ou quanto é 9×4 não faz diferença. O que ele precisava saber é o resultado de 9×8. Então, ele abandona a questão.

Isso pode acontecer com todos nós. Às vezes, nossa memória falha e a ansiedade contribui muito para que isso aconteça.

Você percebe o quanto é importante compreender antes de memorizar?

Agora, vamos conhecer algumas estratégias e refletir sobre como ensinar tabuada para as crianças, priorizando a compreensão.

1.     Ensinar a tabuada da maneira correta

Você aprendeu tabuada da maneira a seguir?

Essa é a tabuada do 4, certo?

Porém, quando dizemos “quatro vezes um”, estamos nos referindo a repetir o número 1 por 4 vezes (1+1+1+1). E quatro vezes o número dois (2+2+2+2). Continuando, quatro vezes o número três (3+3+3+3). E assim por diante.

Pense comigo: se essa é a tabuada do 4, por que o número 4 não está se repetindo?

E se eu colocar a tabuada assim:

Podemos compreender dessa forma: “uma vez o número 4” (4), “duas vezes o número 4” (4+4), “três vezes o número 4” (4+4+4).

Qual fator que se repete? Aí sim! Essa é a tabuada do 4!

Você pode estar pensando: isso é besteira ou um modismo, pois só muda a ordem e o resultado permanece o mesmo.

No entanto, para quem está aprendendo, ensinar a tabuada dessa última maneira faz muito mais sentido. Experimente!

2.     Começar com significados mais simples

A BNCC prevê para o 2º ano, a ideia de adição de parcelas iguais. Por exemplo: 5 + 5 + 5 = 3 x 5. No 3º ano, além da adição de parcelas iguais, há a ideia de disposição retangular.

Já no 4º Ano, acrescenta-se a ideia de proporcionalidade e no 5º Ano, combinatória. Também no 5º Ano, são introduzidos os números decimais.

Alguns autores sugerem que é melhor começar o ensino com problemas que envolvem a proporcionalidade, pois as crianças têm mais facilidade de compreender essa ideia.

Por exemplo, essa camisa tem 5 botões. Para fazer 3 camisas iguais, quantos botões irei precisar?

Problemas com dobro, triplo, também ajudam a trabalhar o significado da proporcionalidade.

O ideal é iniciar a aprendizagem com cálculos por contagem e progredir até o cálculo formal.

3.     Utilizar materiais concretos e imagens

Quando as crianças começam a aprender qualquer operação, os materiais concretos ajudam bastante.

Com a tabuada não é diferente. Por isso, se as crianças estão começando a aprender multiplicação ou ainda não compreenderam o significado, utilize materiais concretos.

Pode ser:

• Material Dourado,
• Escala Cuisenaire,
• Tampinhas,
• Caixa de ovos,
• Potinhos,
• Pedrinhas, grãos de milho ou feijão.

Enfim, inúmeras possibilidades.

Para isso, se atente sempre à maneira mais adequada de ensinar a tabuada.

Por exemplo, 2×3: vamos fazer dois grupinhos com três cubinhos cada. Assim, na tabuada do 3, a quantidade de cubinhos vai permanecer a mesma (3). O que vai alterar são os grupinhos.

Ou 5×4: vamos usar 5 tampinhas e colocar 4 grãos de milho em cada tampinha. Depois, contamos o resultado total. Assim, na tabuada do 4, a quantidade de milhos vai permanecer a mesma (4). O que vai alterar é a quantidade de tampinhas. Pois, é a tabuada do 4.

O Material Cuisenaire também é muito útil para ensinar esse conceito.

Por exemplo, para representar 5×2, vamos pegar 5 barrinhas vermelhas. Qual barrinha tem o mesmo tamanho das cinco barrinhas vermelhas? Os alunos podem comparar e vão perceber que a barrinha laranja tem o mesmo tamanho. Sendo assim, 5×2=10.

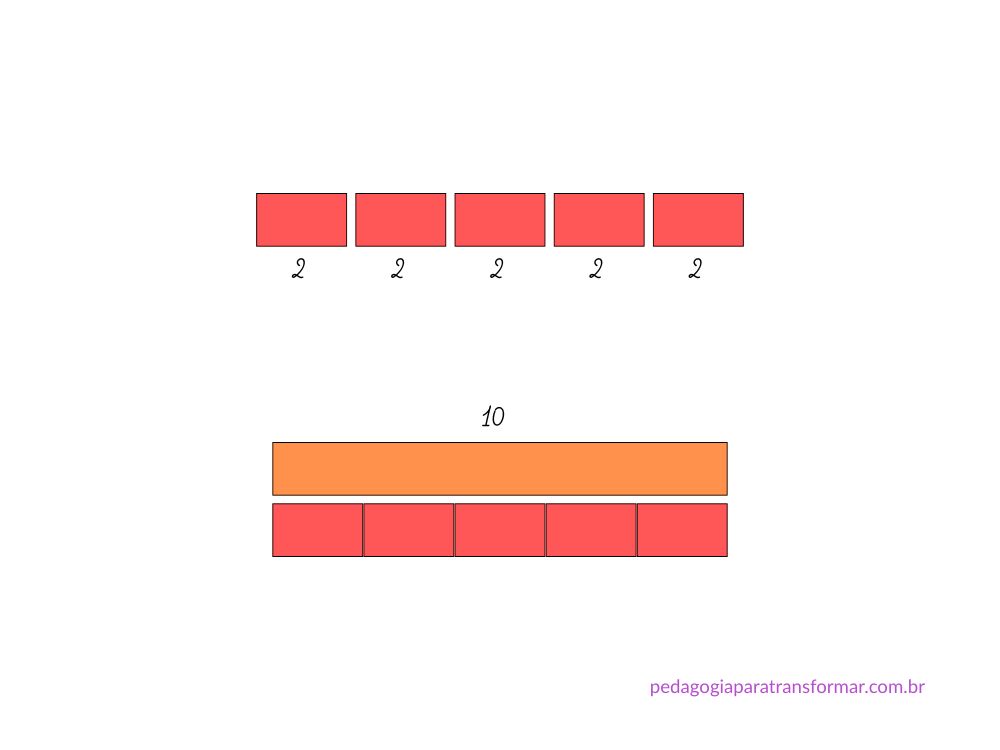
Depois que as crianças já tiveram contato com o concreto, podemos utilizar imagens.

4.     Reta numérica para ensinar tabuada

Com a reta numérica podemos ajudar os alunos a visualizar a multiplicação como soma repetida.

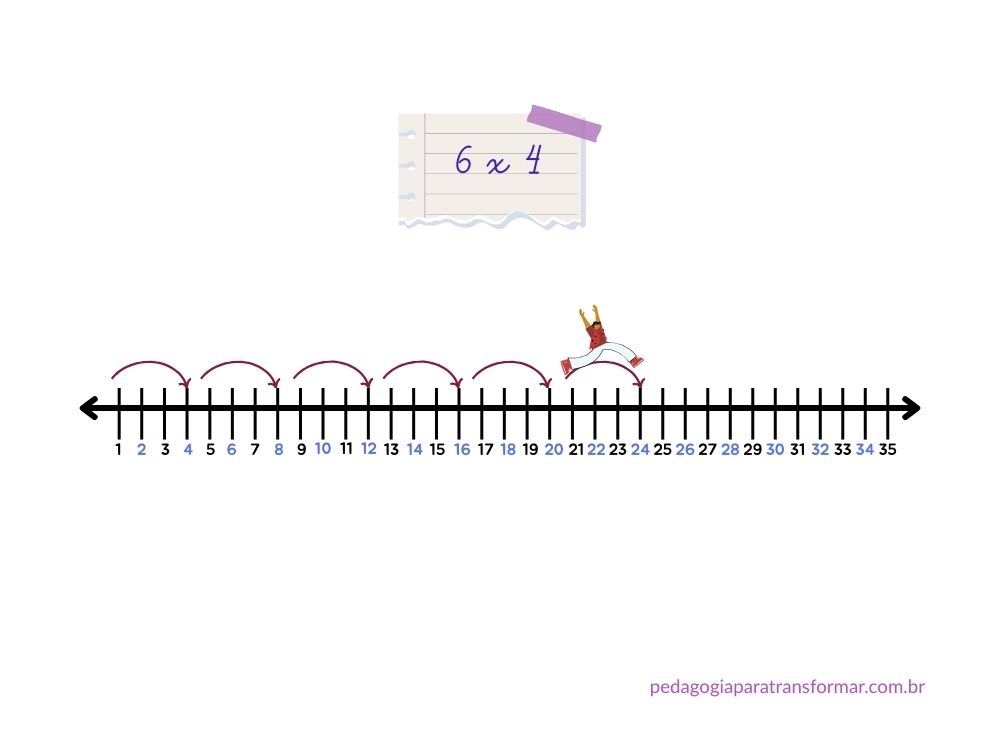
Alguns jogos bem conhecidos ajudam a tornar esse aprendizado divertido, como sortear uma carta com a quantidade de pulos e outra com o comprimento dos pulos.

Pode ser realizado com uma reta fixada no chão ou em uma folha de atividades.

Ao marcar saltos de mesmo tamanho na reta, cada passo representa uma adição repetida. Esse procedimento reforça o entendimento do significado da multiplicação e facilita a memorização das tabuadas, além de desenvolver o raciocínio lógico e a orientação espacial.

Utilizando a reta numérica, os estudantes conseguem observar padrões e regularidades.

5.     Malha quadriculada para ensinar tabuada para crianças

A malha quadriculada permite ver os resultados da multiplicação como área. Dessa forma, é possível abordar a tabuada por meio da geometria e reforçar a ideia de configuração retangular.

Disponibilize uma folha quadriculada para os alunos. Para tornar a atividade mais divertida você propor jogos.

Por exemplo, as crianças jogam dois dados. Conforme o resultado que sair, elas colorem os quadradinhos da malha quadriculada ou desenham bolinhas e verificam o resultado.

Cada um dos jogadores pode usar uma cor de lápis. No final, eles podem somar os próprios resultados e observar quem conseguiu colorir mais quadradinhos.

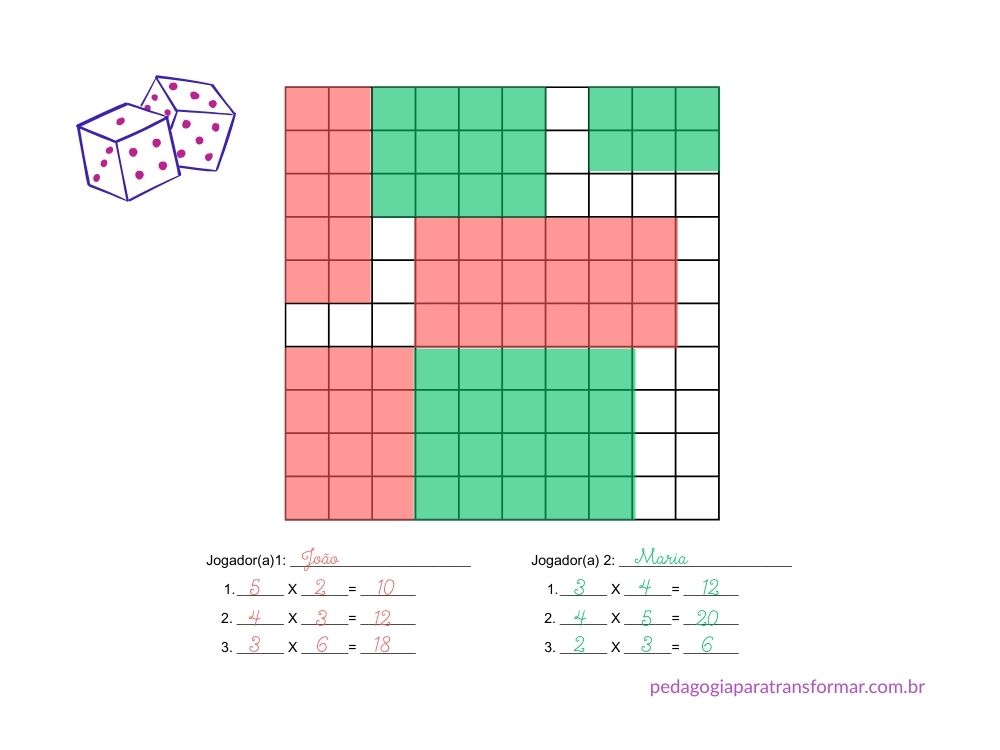
6.     Tabuada em tiras

Entregue uma tira de papel e peça para os alunos numerarem. Ou disponibilize a tira já numerada. Por exemplo, para trabalhar a tabuada do 2, numerada até 20.

Em seguida, peça para contarem de 2 em 2, colorindo sempre o 2º quadradinho.

Depois, devem recortar cada quadradinho pintado, um de cada vez, e colar um embaixo do outro. Com esse resultado obtido, podem completar a tabuada do 2.

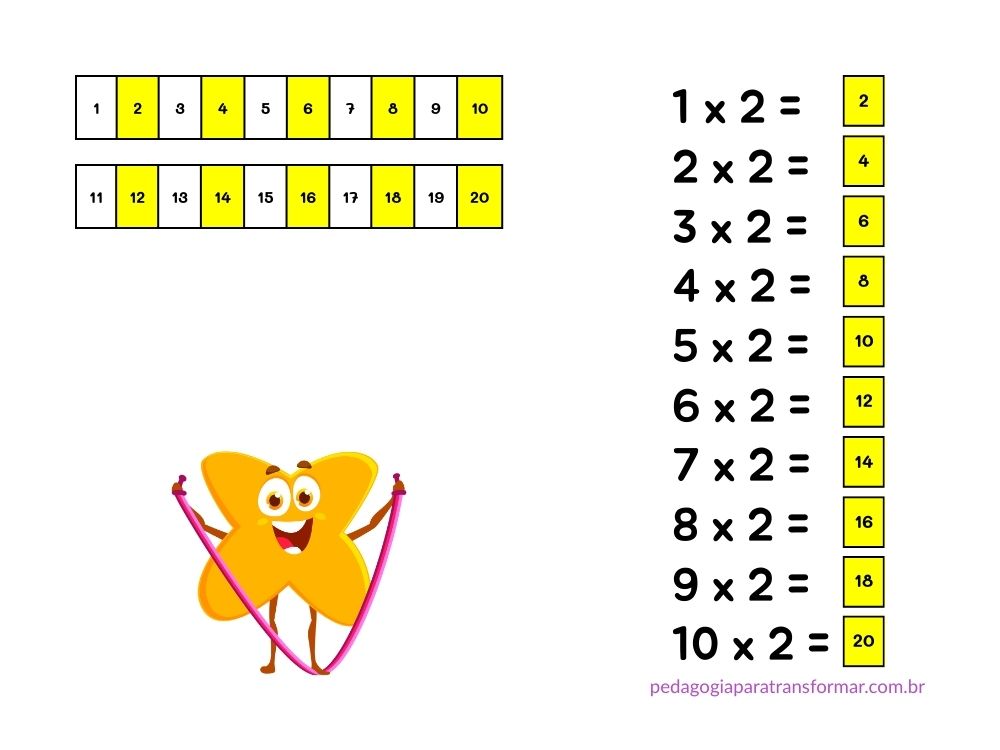
O mesmo procedimento pode ser feito para todas as tabuadas. Para não confundir, pode ser realizado ao longo de semanas.

A atividade pode ser realizada individualmente, em que cada um constrói sua própria tabuada. Mas, também é possível realizar de modo coletivo, fazendo uma tabuada grande para colar no papel pardo e expor na parede.

Variação: Faça trilhas no chão com papel ou fita adesiva. Cada passo representa um número. Exemplo: para “contar de 2 em 2”, os alunos saltam pulando nos números 2, 4, 6, 8, etc.

7. Tabela da tabuada

Entregue uma tabela em que cada coluna é uma tabuada. Ou seja, a primeira coluna é reservada à tabuada do 1. Na segunda coluna, a tabuada do 2.

Mas, tem um detalhe: a tabuada do 2 deve começar em 2×2, a tabuada do 3 deve começar em 3×3 e assim por diante. Daqui a pouco você vai compreender melhor o porquê dessa estratégia.

Peça para os alunos completarem as multiplicações, utilizando alguma estratégia já trabalhada (pode ser alguma das sugestões anteriores). Não é preciso completar a tabela de uma vez só, podemos trabalhar uma coluna a cada dia, por exemplo.

Quando terminarem essa tarefa inicial, devem preencher os espaços em branco. Para isso, dê uma dica: todas as multiplicações que estão faltando já têm a resposta preenchida anteriormente.

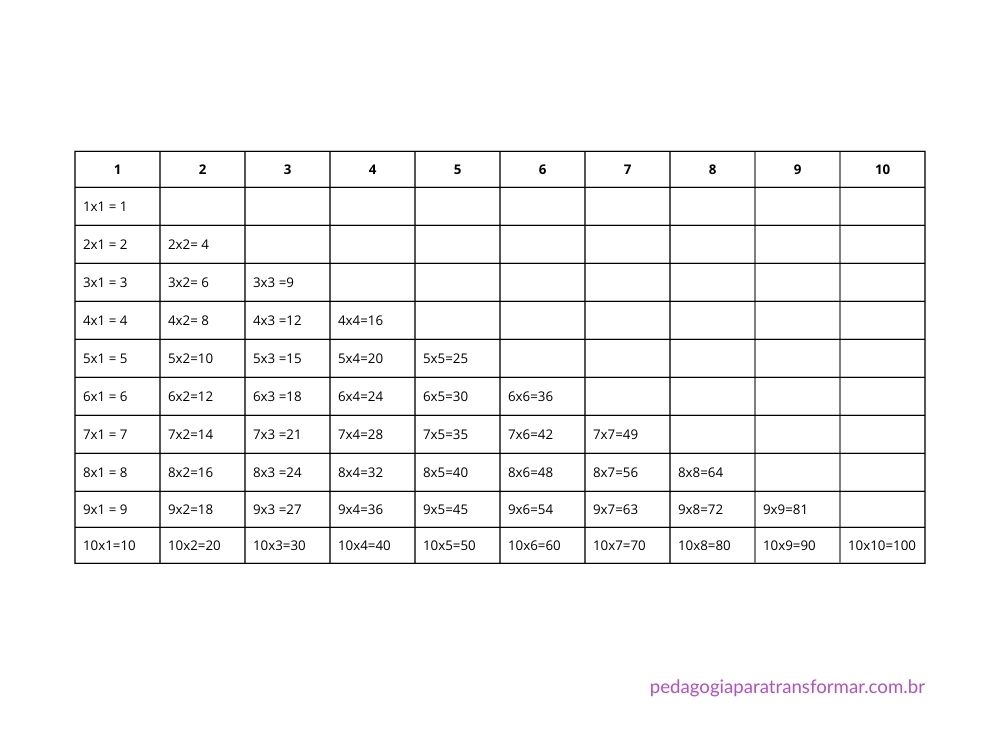
Por exemplo, para saber quanto é 2 x 1, podemos voltar na tabuada do 1 e perceber que 1×2=2. Sendo assim, o resultado será o mesmo.

Essa atividade é importante para as crianças perceberem a propriedade comutativa da multiplicação, ou seja, a ordem dos fatores não altera o produto. (Na minha turma de escola, costumávamos dizer que a ordem dos tratores não altera o viaduto 😄Na sua turma também tinha essa brincadeira?)

Depois da tabela pronta, os alunos podem colar no caderno e utilizar quando necessário.

8.     Estimular a observação das regularidades da tabuada

Começar ensinar a tabuada do 2, 5 e 10 facilita o processo. Pois, é mais fácil de observar as regularidades nessas tabuadas. Nessa perspectiva, é um equívoco ensinar as tabuadas em ordem começando do 1 até o 10.

Incentive os alunos a observarem quais algarismos se repetem ao final dos resultados da tabuada.

O que nos parece óbvio pode não ser para as crianças. Por isso incentive-as a perceber que:

• Por exemplo, na tabuada do 3, 3×1 é menor que 3×2, que por sua vez, é menor que 3×3. Os valores aumentam de 3 em 3. Isso acontece com todas as tabuadas, os valores variam de 1 em 1 na tabuada do 1, de 2 em 2 na tabuada do 2 e assim, por diante.

Dessa forma, as crianças entendem a ideia de proporcionalidade na multiplicação.

• Há uma relação entre as tabuadas. Por exemplo, se 2×8=16, logo 4×8=32, pois 4 é o dobro de 2, logo, os resultados da tabuada do 4 vão ser o dobro da tabuada do 2 (16+16=32).
• Assim como os resultados da tabuada do 9, são o triplo da tabuada do 3. Entre outras possibilidades de relacionar uma tabuada com outra.
• Os resultados da tabuada do 10 terminam em 0. Sendo assim, todo número multiplicado por 10, termina em 0.
• Os produtos da tabuada do 5 terminam em 5 ou 0. Então, todo número multiplicado por 5, termina em 5 ou 0.
• Todo número multiplicado por 1 tem como resultado ele mesmo.
• A soma dos produtos da tabuada do 2 e do 3 corresponde aos resultados da tabuada do 5. Sendo assim, matematicamente 5×9 pode ser escrito da seguinte forma: (2×9) + (3×9) = 18 + 27 = 45. Essa é a propriedade distributiva.
• Outro exemplo, se o aluno esquecer a tabuada do 7, ele pode somar os produtos da tabuada do 2 e do 5, que são mais fáceis de aprender.

9. Expor um painel na sala de aula com a tabuada de Pitágoras

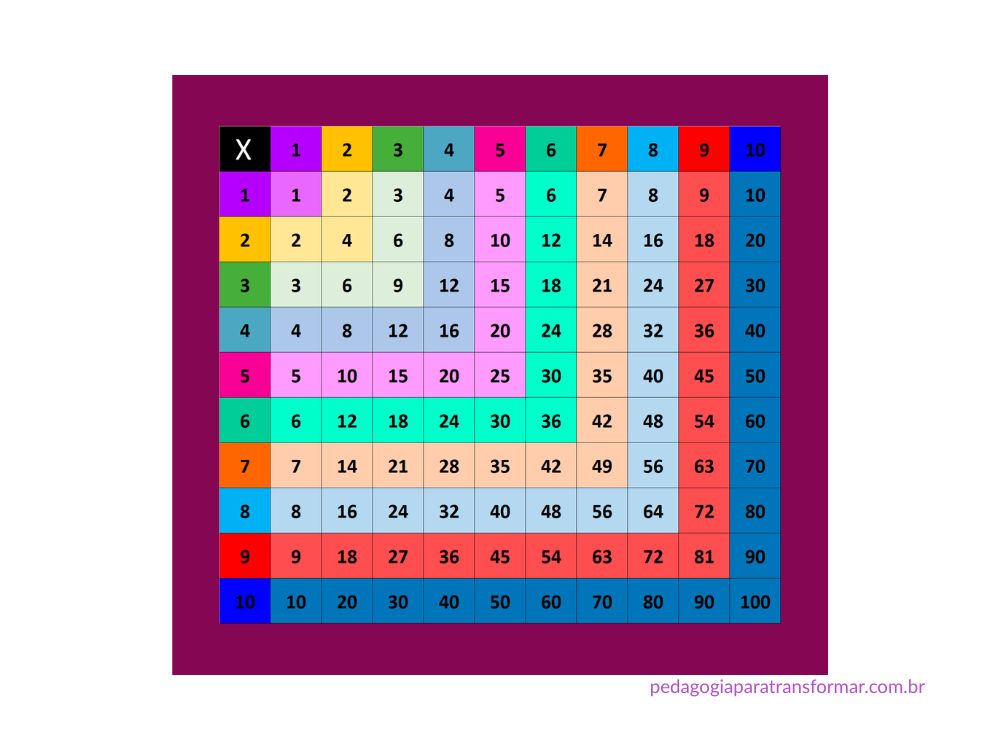
A tabela de Pitágoras permite que o aluno veja toda a estrutura da multiplicação de forma clara e organizada. Ele pode observar, por exemplo:

• Que 3 × 4 = 4 × 3 (propriedade comutativa);
• Que as diagonais crescem simetricamente;
• Que as multiplicações se repetem em ordem lógica.

É interessante confeccionar a tabuada com a turma, pois assim eles conseguem perceber como ela é construída.

Além disso, cada aluno pode ter a sua própria tabela de Pitágoras, plastificada e com dois elásticos: um na vertical e outro na horizontal. Se um aluno esquecer quanto é 6 × 7, ele pode buscar o número cruzando o elástico na linha do 6 com a coluna do 7. Esse é o princípio da comutatividade.

Com o tempo, ele se acostuma com os padrões e reconhece o resultado com maior segurança.

Estimule os estudantes a observar que se memorizarmos somente a metade da tabela de Pitágoras, conseguimos resolver todas as tabuadas. Pois, os resultados se remetem a partir de um eixo de simetria diagonal no centro da tabela.

A Tabela de Pitágoras pode ser usada em aulas diversas para:

• Trabalhar múltiplos;
• Encontrar quadrados perfeitos;
• Explorar divisibilidade (através da inversão da multiplicação);
• Introduzir propriedades da multiplicação.

Conclusão

Como vimos, há muitas possibilidades que sugerem como ensinar tabuada para crianças. Você pode escolher alguma das estratégias citadas aqui ou utilizar outras.

Mas, o mais importante é ajudar as crianças a dominarem o conceito antes de memorizar. Essa é a reflexão principal deste post.

Após desenvolver atividades com materiais concretos, reflexões e troca de ideias entre os alunos, proponha atividades de sistematização para fixar e registrar o que aprenderam.

Você vai gostar de ler: Estratégias de cálculo mental: multiplicação e divisão

Referências

MICARELLO, Hilda (Org.). Formação em rede. Juiz de Fora: FEME, 2010.

São Paulo (SP). Secretaria Municipal de Educação. Coordenadoria Pedagógica. Orientações didáticas do currículo da cidade: Matemática – volume 1. – São Paulo: SME / COPED, 2018.