Confira várias ideias para ensinar frações de forma divertida e favorecer a aprendizagem ativa, com compreensão.
Olá! Que bom ter você aqui!
Seus alunos apresentam dificuldade em compreender frações? Parece que as ilustrações do livro didático não fazem muito sentido para eles?
Pois é, isso é muito comum.
Na verdade, é difícil para nós, educadores, explicar frações de forma contextualizada e divertida porque geralmente aprendemos frações de forma mecânica, colorindo as partes de um círculo desenhado.
A impressão que eu tinha era de que fração só existia no papel e estava muito distante da vida real. Você também aprendeu assim?
Diante disso, muitas vezes temos que refletir sobre o conceito de fração e buscar novas estratégias para aproximar o estudo de frações às situações reais e significativas.
Convido você a refletir sobre frações e conhecer várias ideias para ensinar frações de forma divertida e significativa.
Por que fração é tão difícil para os alunos?
Se pararmos para refletir, é perfeitamente compreensível que os alunos tenham dificuldades em entender frações.
Eles foram acostumados com os números naturais, sabem que os números representam quantidades e que quando contamos os números vão aumentando.
As frações surgem como algo novo, que não segue as mesmas regras que eles já aprenderam. Por exemplo, ½ de uma pizza grande é diferente de ½ de uma pizza pequena. Ou ½ de uma folha de papel não é o mesmo que ½ de quatro folhas.
Outra questão é que quando o denominador de uma fração aumenta, seu valor diminui. Para as crianças, é difícil compreender que 1/3 é maior que 1/5, pois aprenderam que cinco é maior que três.
Sendo assim, o aprendizado dos números racionais pode causar um certo desconforto aos alunos.
Algumas ideias iniciais que devemos trabalhar com os alunos:
- As frações surgiram da necessidade de medir
- Quando dividimos um todo em partes menores, para indicar fração é necessário que essas partes sejam matematicamente iguais
Você pode explicar com exemplos: Imagine que você e outro colega ganharam uma torta deliciosa de chocolate em um sorteio e precisam dividi-la. O que você acha se um colega tirar um pedacinho fininho para você e ficar com o restante da torta? Ele dividiu em 2 partes, não é mesmo?
Certamente o aluno vai dizer que não é justo e que a torta tem que ser dividida em partes iguais. E então, você explica que para ser considerada uma fração, realmente precisamos dividir um todo em partes iguais.
- Um todo pode significar mais de uma coisa
Quando aprendemos frações, ficamos muito presas à ideia de que o todo precisa ser somente uma coisa. Por exemplo, um bolo, uma pizza, uma folha de papel etc.
No entanto, um todo pode significar mais de uma coisa, agrupadas em conjunto. Por exemplo, uma coleção com 30 carrinhos. Você precisa de todos os carrinhos para formar um todo que é a coleção.
Sendo assim, fração também pode ser uma parte de um grupo.
- Enfatizar que frações são números
- Explicar que o numerador e denominador trabalham juntos para criar um único valor.
Uma maneira fácil de explicar é que o denominador (número de baixo) indica quantas partes iguais um todo foi dividido ou em quantos grupos um conjunto foi dividido. O denominador também dá nome a cada uma dessas partes.
Por exemplo, 1/3 significa que o todo foi dividido em 3 partes iguais e cada uma dessas partes é chamada de terço.
Já o numerador (número de cima) indica quantas partes temos. Então, significa que em 1/3 temos 1 de 3 partes ou 1 de 3 grupos.
Para ensinar frações, comece com materiais concretos
Material Cuisenaire
O Material Cuisenaire é ótimo para ensinar frações. Para isso, devemos desapegar da ideia original de que as barrinhas valem de 1 a 10. E passamos a considerar que cada barrinha é um todo.
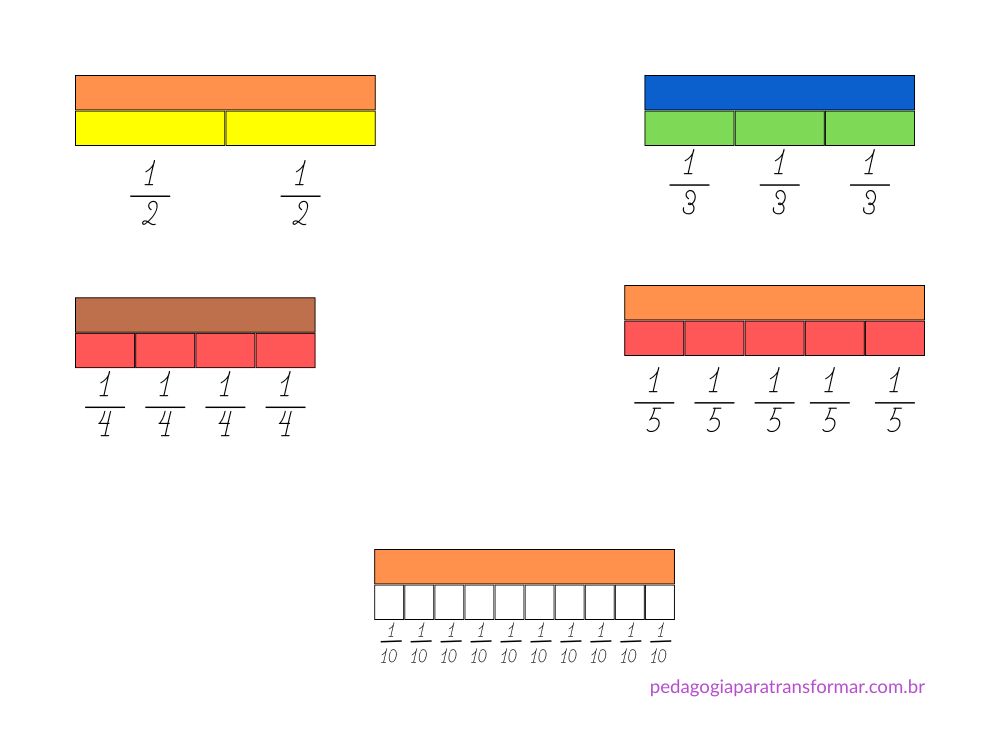
Por exemplo, se considerarmos a barrinha laranja como um inteiro, a barrinha amarela equivale a ½. Cada barrinha vermelha equivale a 1/5. Cada cubinho equivale a 1/10.
Se a barrinha azul for considerada um todo, a barrinha verde equivale a 1/3.
Conjuntos de objetos
Um conjunto de objetos ajuda a compreender que a fração também pode ser parte de um grupo.
Por exemplo, um conjunto com 24 lápis de colorir. Podemos mostrar que se dividirmos os lápis em dois grupos e retirarmos um desses grupos, estamos retirando ½, que equivale a 12 lápis.
Agora se agrupamos em 3 partes e retiramos uma dessas partes, estamos retirando 1/3, que equivale a 8 lápis.

Você também pode trabalhar com situações-problema. Por exemplo: Elisa quer dividir 15 balas com 5 amigas. Se cada uma ficar com 1/5 das balas, quantas balas cada uma ficará?
É importante enfatizar a relação entre frações e divisão.
Frações em tiras
As tiras de frações são muito utilizadas, pois são muito eficientes.
Disponibilize tiras de papel para crianças. Acho interessante utilizar cores variadas e tiras da largura de uma folha A4.
A primeira tira não precisa ser dobrada, pois ela representará o inteiro. Uma sugestão é escrever o número 1 e colar essa primeira tira em uma folha A4 em branco.
No entanto, se você prefere que as crianças modelem as tiras, movendo-as quando necessário, não precisa colar. Sendo que, nesse caso, o ideal é utilizar um papel mais firme.
Peça para as crianças pegarem outra tira, de determinada cor e dobrarem o papel ao meio. Depois, elas devem passar o lápis de escrever marcando o sinal da dobra.
Questione: em quantas partes a tira foi dividida? Esse será o denominador da fração (o número de baixo). Nesse primeiro pedacinho quantas partes temos? Então cada parte é ½ dessa tira de papel.
Depois de escrever as frações, os alunos podem colar essa segunda tira na folha, embaixo da primeira.
A próxima tira será dividida em 3 partes. Gosto de deixar uma marcação para facilitar a dobra em 3, 5, 7 e 9 partes. E assim, por diante, eles vão fazendo as marcações e escrevendo as frações.
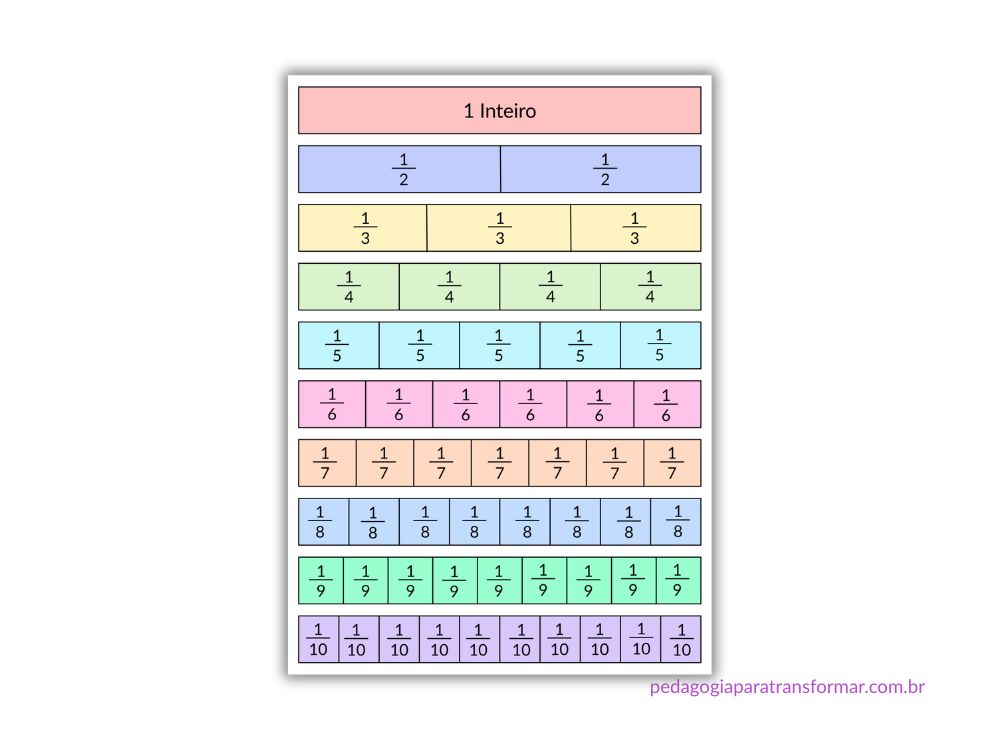
As tiras podem ser usadas para compreender o tamanho das frações. Ao comparar duas tiras, eles conseguem perceber visualmente quais frações são menores ou maiores.
Você pode propor uma atividade de escrita de frases, por exemplo, 1/3 > ¼.
Esse material também será útil para a compreensão de frações equivalentes. Com o auxílio de uma régua, incentive os alunos a observarem, por exemplo, que 2 partes de ¼ (2/4), 4 partes de 1/8 (4/8), 5 partes de 1/10 (5/10) têm o mesmo tamanho de ½ dessa mesma tira de papel.
Como ensinar frações na reta numérica?
Compreender frações na reta numérica também não é algo fácil para os alunos. Uma estratégia para facilitar esse processo é também utilizar materiais concretos. Você pode utilizar as tiras de frações.
Por exemplo, vamos começar com a fração ½. Quantas partes de um meio equivalem a um inteiro?
Depois que eles representarem essa fração utilizando a tira ou outro material concreto, peça para desenharem uma reta numérica abaixo das tiras de fração.
Oriente as crianças a colocarem o número zero no início da reta numérica e o 1 no final, pois o 1 representa 2 meios (2/2) ou 1 inteiro. Certifique se elas compreenderam que a distância entre o 0 e o 1 é igual a 1 inteiro.
Agora que já identificaram a posição do 0 e do 1 na reta numérica, oriente-os a marcar onde acontecem as divisões, no caso das tiras, são as dobras que fizemos e marcamos com lápis.
Se o todo é composto de meios, vamos marcar onde fica ½, ou seja, a metade.
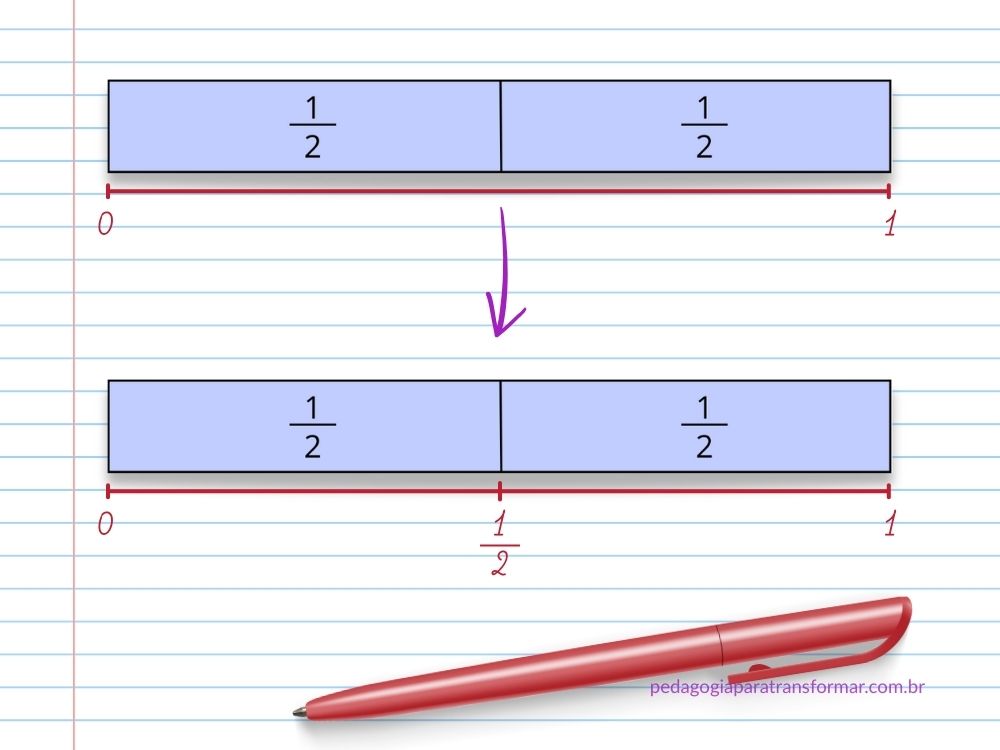
Na segunda tirinha, que foi dividida em três partes, vamos marcar o 0 no início da reta numérica e o 1 que representa 3/3 ou 1 inteiro.
Como a tirinha é composta de terços, vamos marcar 1/3 e 2/3, observando o sinal das dobrinhas e fazendo os tracinhos da reta numérica rente a elas.

E assim, por diante, você pode ajudar as crianças a construírem retas numéricas com as frações mais usuais (1/2, 1/3, ¼, 1/5 e 1/10).

Dessa maneira, quando eles visualizarem a reta numérica nas folhas de atividades, conseguirão compreender o que ela está representando.
Tenho outras sugestões para você!
Uma delas é dividir a turma em grupos e propor que eles façam uma reta numérica grande. Você pode sortear em quantas partes precisam dividir a reta e eles escrevem as frações correspondentes.
Ou sortear algumas frações para eles descobrirem em quantas partes devem dividir a reta numérica e em quais posições precisam colar frações escritas em pedacinhos de papel ou post-it.
Os cartazes podem ser expostos na parede da sala de aula para servir de consulta quando precisarem.
Outra sugestão é fazer uma reta numérica humana. Cada aluno segura uma fração e se posiciona na reta desenhada no chão.
Jogos com frações
Há muitas possibilidades de ensinar ou reforçar o aprendizado de frações com jogos:
- Jogo de trilha com frações
- Dominó de frações
- Bingo de frações
- Jogo Papa-Tudo de frações
Esse último é um dos meus jogos favoritos. Você prepara cartinhas com frações variadas e distribui com os jogadores, como se fosse um baralho.
As crianças não veem as cartas, que são colocadas em pilha com os números virados para baixo, sobre a mesa.
Ao sinal, cada aluno deve virar a carta de cima de sua pilha, todos ao mesmo tempo. O objetivo é verificar em qual carta está representada a maior fração. O jogador que tiver a carta com a maior fração fica com todas as cartas, isto é, “papa-tudo”.
Caso sejam viradas duas ou mais cartas com o mesmo valor, elas permanecem na mesa para a próxima rodada.
O jogo termina quando as cartas acabarem. Vence quem terminar com mais cartas.
Uma sugestão é utilizar as tiras de frações como apoio para o jogo. Geralmente, os alunos ficam em dúvida em identificar qual fração é maior. Assim, eles podem consultar as tiras de frações, inclusive marcando com a régua para facilitar a comparação.
Esse “detalhe” favorece a autonomia, pois em vez de perguntar à professora, eles aprendem a buscar as respostas.
Relacionar frações a contextos da vida real
Estimule os estudantes a perceberem que as frações estão presentes no nosso cotidiano.
Por exemplo, quando dizemos as horas, 10h e meia, a palavra “meia” está se referindo à metade de uma hora.
Quando vamos fazer uma receita é comum encontrar frações: ½ xícara, 1/3 de xícara, ¼ de xícara.
Leve copos medidores para a sala de aula e permita que as crianças observem a relação entre eles, testem, por exemplo, que 3 medidas de 1/3 cabem em um medidor de 1 xícara.

Conclusão
Agora que você já sabe como ensinar frações de forma divertida, o próximo passo é colocar em prática!
Dessa forma, as crianças podem aprender frações de forma leve, observando, manipulando os materiais concretos, experimentando, fazendo descobertas. Enfim, de maneira ativa e com compreensão.
Você que gosta de ensinar matemática de forma criativa, vai gostar de ler: Como ensinar tabuada para crianças, de forma simples e com compreensão

