Conheça várias estratégias de cálculo mental para ensinar multiplicação e divisão, priorizando a compreensão antes da memorização do algoritmo.
Você percebe que os alunos sentem muito mais dificuldade em compreender a multiplicação e divisão do que adição e subtração?
Muitos têm pavor quando se deparam com um problema de divisão.
É inquestionável a importância de saber utilizar o algoritmo tradicional. Porém, sabemos que utilizá-lo sem compreender o significado da multiplicação e divisão, não garante sucesso na aprendizagem.
Grande parte dos estudantes não consegue resolver as operações básicas porque encontram muita dificuldade em seguir os procedimentos convencionais.
Diante dessa realidade, temos que procurar novas estratégias para melhorar o ensino e aprendizagem.
Contudo, a maioria de nós, aprendeu matemática por meio de um ensino tradicional. É difícil pensar em outras possibilidades de ensinar, não é mesmo?
Por isso, reuni neste post, diversas estratégias de cálculo mental para ensinar multiplicação e divisão, prezando principalmente o cálculo mental. O intuito é que você conheça possibilidades para ajudar alunos com dificuldade de aprendizagem.
Além de mostrar para eles que não existe uma única forma de resolver problemas matemáticos e que por isso, todos nós somos capazes de aprender matemática, superando nossas limitações e respeitando nosso estilo e ritmo de aprender.
O que é cálculo mental?
Quando você lê “cálculo mental” logo pensa em “fazer conta de cabeça” e de forma rápida?
Essa é uma visão restrita que foi transmitida para nós.
O cálculo mental é , na verdade, um processo pensado, em que o aluno utiliza estratégias, decomposições e raciocínio lógico.
Por isso, ao ensinar cálculos mentais para os alunos podemos usar lápis e papel sim!
No cálculo mental, a rapidez não é o objetivo principal. O foco está em compreender o que está acontecendo com os números e encontrar caminhos eficientes para chegar ao resultado.
Isso significa que o aluno pode pensar em etapas, fazer ajustes, reorganizar números e até verificar a resposta antes de concluir.
Essa abordagem estimula a flexibilidade matemática, pois mostra que não existe apenas um jeito de resolver, e que cada pessoa pode escolher a estratégia que fizer mais sentido para o seu raciocínio. Com o tempo e a prática, a fluidez aumenta naturalmente.
Por que é importante ensinar estratégias alternativas de cálculo?
Primeiramente, como podemos observar na prática, a memorização da tabuada e do algoritmo, por si só, não garante a aprendizagem da multiplicação e divisão.
Alguns alunos têm facilidade de memorizar, mas não conseguem aplicar esse conhecimento na resolução de problemas porque não compreendem o sentido por trás do algoritmo.
Outros estudantes, porém, não conseguem memorizar os procedimentos convencionais. E desconhecem outras maneiras de resolver esses cálculos.
Quando apresentamos estratégias de cálculo mental para multiplicação e divisão, estamos oferecendo oportunidades de aprendizagem para todos os alunos, independentemente das suas dificuldades.
Além disso, eles começam a perceber que o algoritmo não “surgiu do nada” e a entender o que estão fazendo e por quê.
Isso não significa que os estudantes devem memorizar e utilizar todas as estratégias, mas ser preparados para utilizar a mais adequada a cada contexto.
Como podemos contribuir com a compreensão da multiplicação e divisão?
- Comece com materiais concretos, como materiais reaproveitados ou criados para este fim, como o Material Dourado e a Escala Cuisenaire.
- Ajude as crianças a representar no papel o que fizeram com o Material Concreto.
- Proponha atividades de sistematização.
- Aos poucos, quando tiverem compreendido o sentido das operações, passe para representações abstratas utilizando o algoritmo.
Estratégias de cálculo mental para multiplicação
Agora vamos conhecer algumas estratégias alternativas de cálculo para multiplicação.
1. Decomposição (distributiva)
Exemplo: 23 × 4
Passo a passo:
- Peça para o aluno decompor o número 23:
→ 20 + 3
- Em seguida, multiplicar em partes:
→ 20 × 4 = 80
→ 3 × 4 = 12
- Finalmente, juntar tudo:
→ 80 + 12 = 92
Observe que o Material Dourado facilita a visualização e compreensão. Após propor uma atividade com material concreto, você pode propor o registro no caderno.
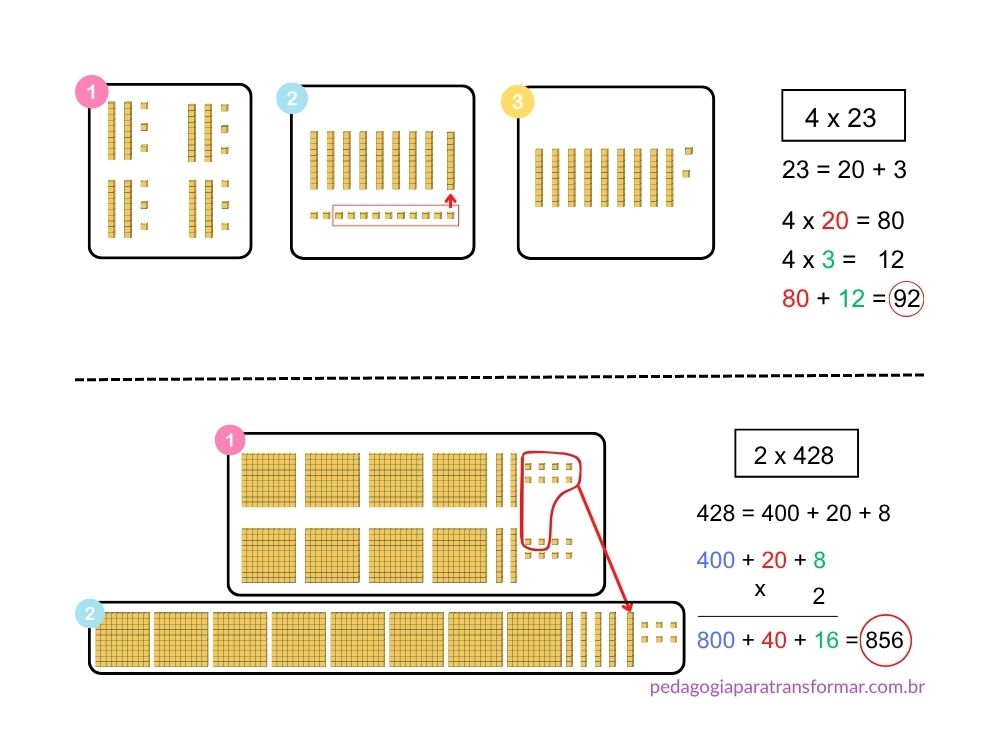
Ao decompor e multiplicar cada parte, o aluno vê exatamente a origem de cada produto parcial. Uma estratégia muito útil para compreensão da propriedade distributiva da multiplicação, que está “por trás” do algoritmo tradicional.

2. Retângulo (técnica italiana)
Exemplo: 14 × 12
Passo a passo:
- Ajude o aluno a escrever a multiplicação de forma decomposta: (10 + 4) × (10 + 2)
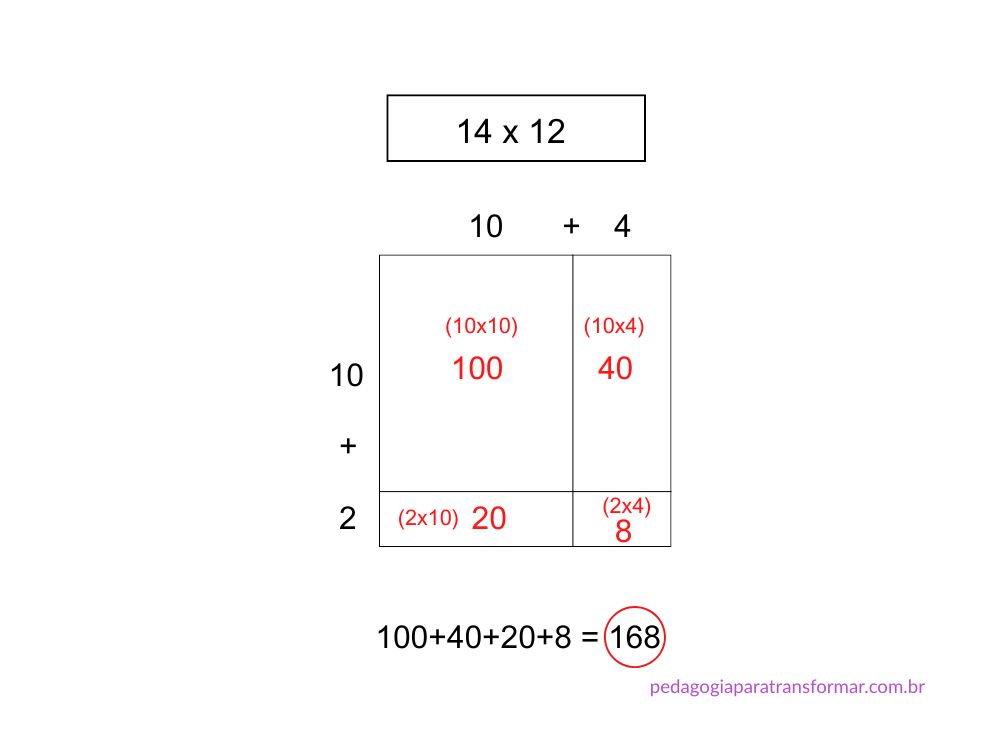
- Proponha a montagem de um retângulo dividido em linhas e colunas para dispor os números decompostos. Em seguida, multiplicar todos os valores entre si.
10×10 = 100
10×2 = 20
4×10 = 40
4×2 = 8
• Finalmente, somar tudo:
→ 100 + 20 + 40 + 8 = 168
Essa é uma ótima estratégia para visualizar o conceito de área e decomposição.
3. Reta numérica com “pulos”
Exemplo: 6 × 4
Essa estratégia é útil para facilitar a compreensão da multiplicação com adição repetida.
Passo a passo:
- Disponibilize uma reta numérica.
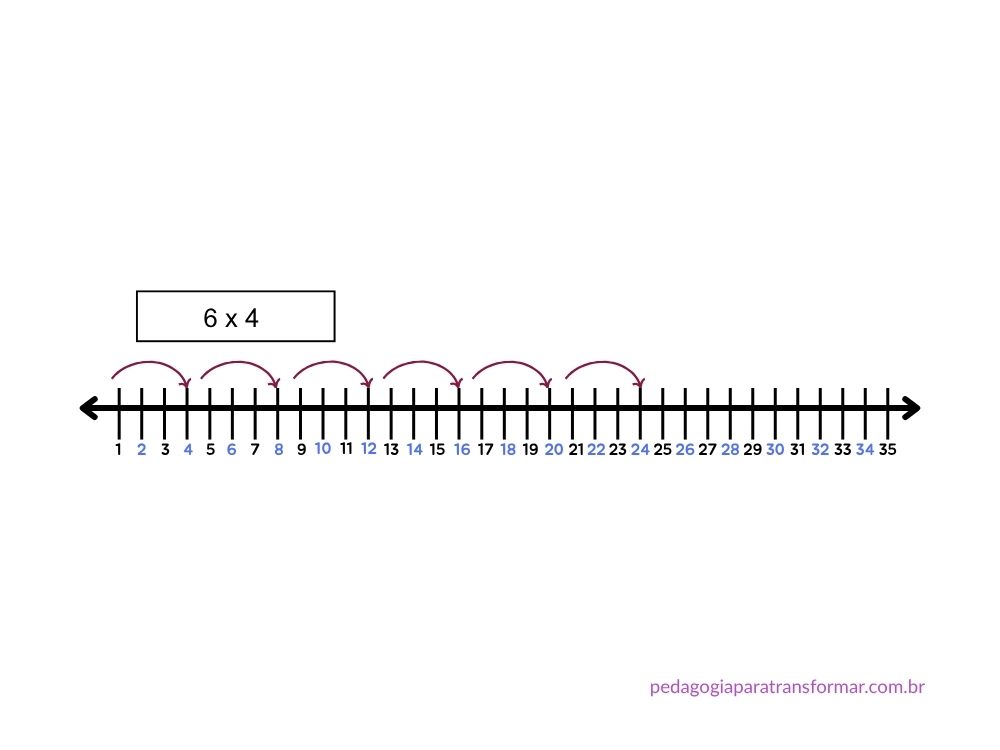
- Desafie o aluno a desenhar 6 “pulos” de 4 passos em uma reta numérica:
0 → 4 → 8 → 12 → 16 → 20 → 24
Resultado: 24
4. Malha quadriculada
Exemplo: 9 x 3
Passo a passo:
- Disponibilize uma malha quadriculada para os alunos.
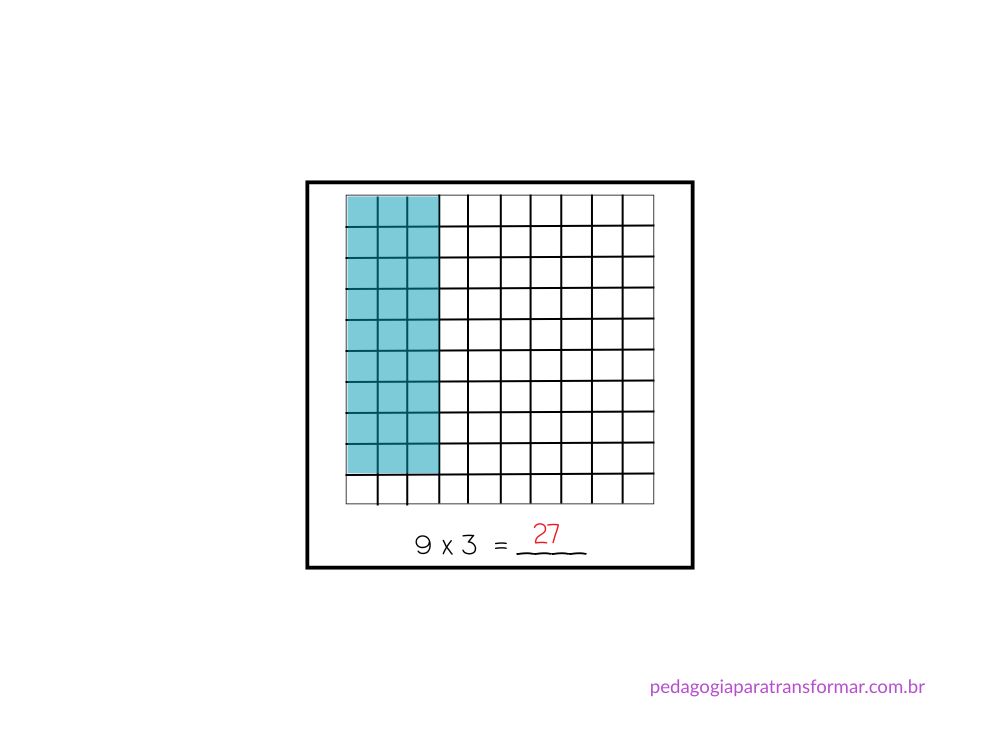
- Peça para desenharem na malha quadriculada:
- Um retângulo com 3 linhas e 9 colunas.
- Depois, só precisam contar as células:
- Cada célula representa 1 unidade.
- Conte todas as células da malha: 27.
Resultado:
→ 3 × 9 = 27
Essa estratégia ajuda a ver a multiplicação como uma área formada por linhas e colunas, reforçando a ideia de que multiplicar é somar grupos iguais.
Estratégias para Divisão
1. Fazer grupos (divisão concreta)
Essa é uma estratégia muito utilizada, pois facilita a compreensão do conceito de divisão de forma simples e eficiente.
Exemplo: 12 ÷ 3
Passo a passo:
- Peça para a criança desenhar 12 bolinhas
- Depois, agrupar em grupos de 3
- Pergunte: quantos grupos você formou? → 4
Você pode utilizar desenhos ou materiais concretos. Por exemplo, dividir 12 grãos de milho em três tampinhas. Quantos grãos de milho ficaram em cada tampinha?
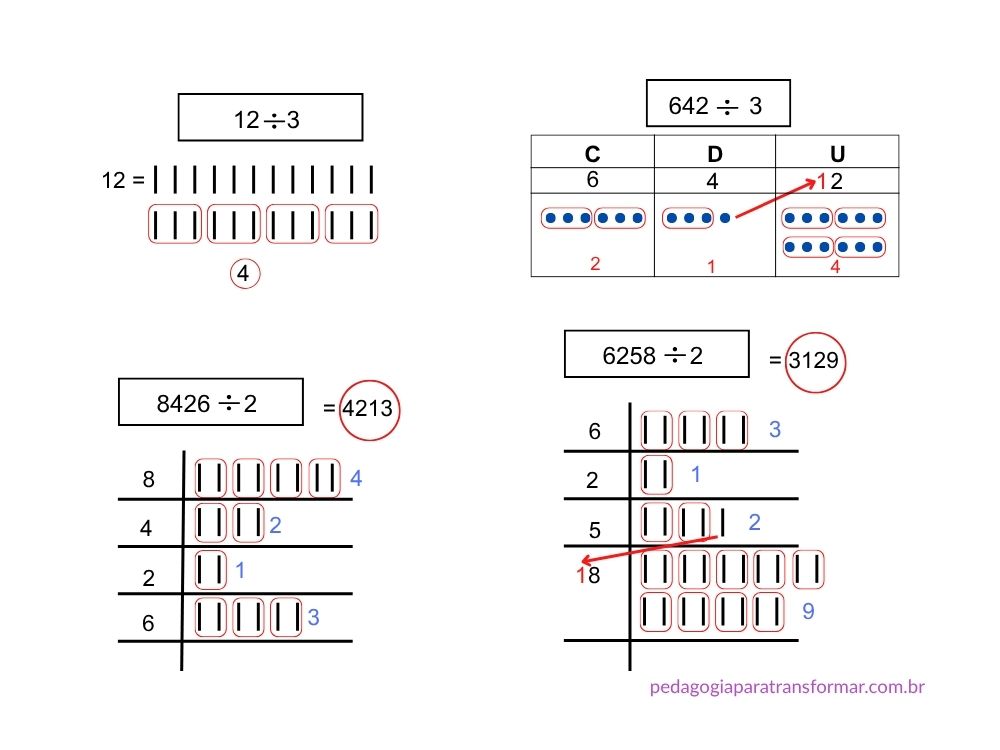
Com números maiores, podemos pedir para as crianças representarem cada número separadamente. A limitação é que não podemos considerar o valor posicional.
Mas, quando a criança tem muita dificuldade, ele pode fazer esses grupinhos para que se sinta mais segura para posteriormente, usar o algoritmo convencional.
2. Contagem para cima (fatores)
Essa é uma boa estratégia para reforçar a tabuada e sentido de “quantas vezes cabe”.
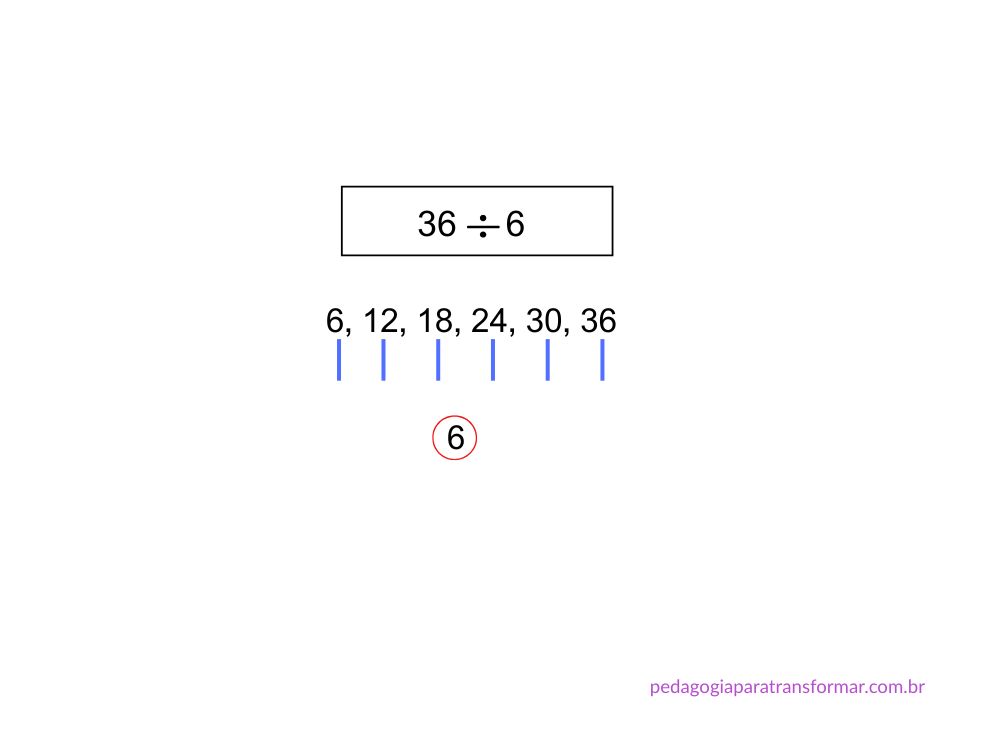
Exemplo: 36 ÷ 6
Passo a passo:
- Pedir para o aluno contar de 6 em 6 até 36:
→ 6, 12, 18, 24, 30, 36
- Quantas vezes você contou? → 6
3. Decomposição
Exemplo: 84 ÷ 4
Passo a passo:
- Peça para o aluno decompor o número 84 em dezenas e unidades:
→ 80 + 4
- Depois, dividir em partes:
→ 80 ÷ 4 = 20
→ 4 ÷ 4 = 1
Resultado: 20 + 1 = 21

4. Fatoração reversa
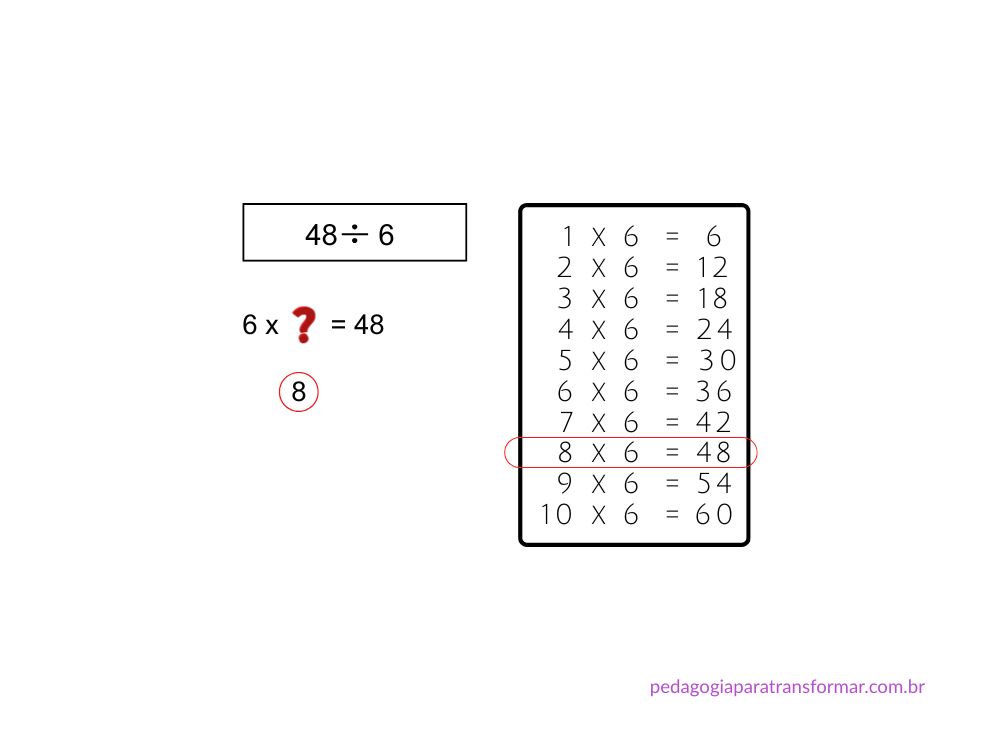
Exemplo: 48 ÷ 6
Passo a passo:
Para essa estratégia, é importante que o aluno saiba a tabuada “de cor” ou tenha uma tabuada para consulta.
- Questione: “seis vezes quanto, dá o resultado 48?”
“6 × ? = 48”
- Ele pode buscar na memória ou consultar uma tabuada para descobrir que:
Se 6 × 8 = 48, logo, 48 ÷ 6 = 8
Divisão utilizando materiais concretos
O Material Dourado e a Escala Cuisenaire são ótimos recursos para trabalhar a compreensão da divisão.
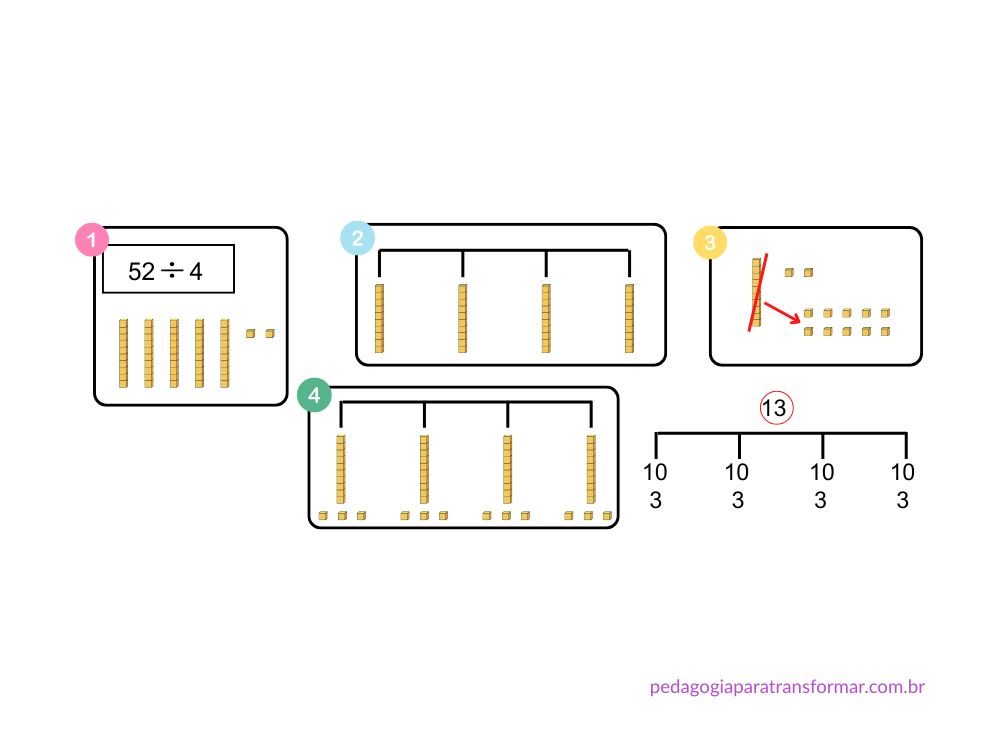
Observe estes exemplos:
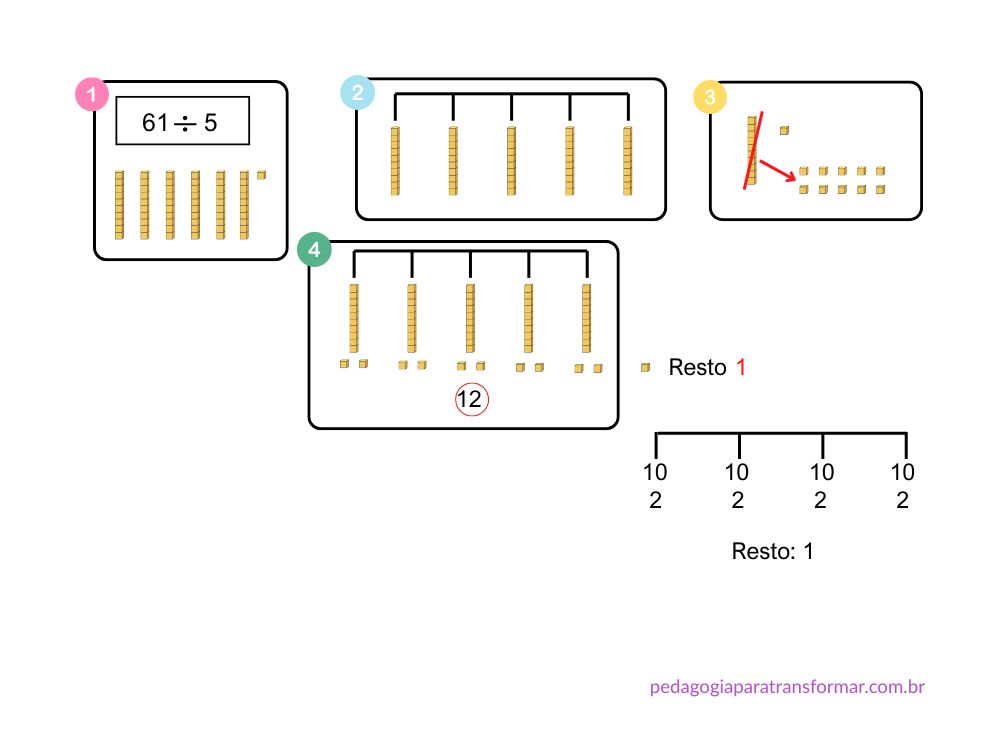
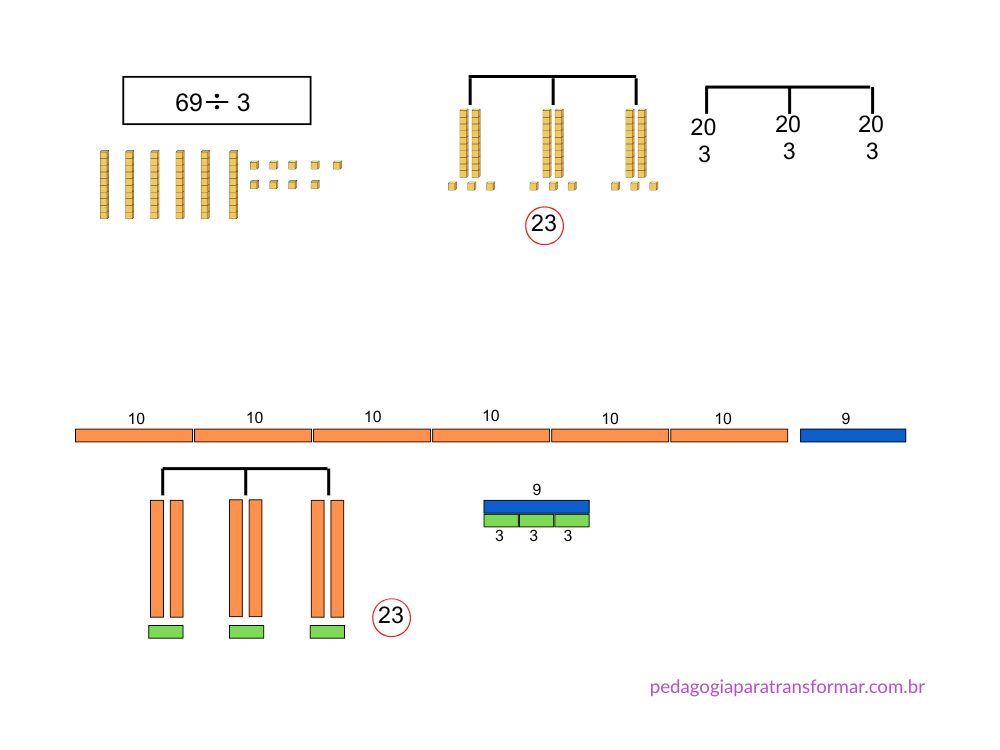
Como aplicar as estratégias de cálculo mental na sala de aula?
- Use material concreto (blocos, tampinhas, palitos, desenhos)
- Explore o quadro/lousa para construir os cálculos com os alunos
- Trabalhe com jogos que reforcem as estratégias (dominós, bingo, trilhas)
- Estimule os alunos a escolher a estratégia com que se sentem mais confortáveis
Conclusão
Enfim, são muitas as possibilidades de estratégias de cálculo mental para multiplicação e divisão.
A multiplicação e a divisão não precisam ser apresentadas apenas como tabuadas decoradas ou algoritmos prontos para aplicar.
Quando priorizamos a compreensão do processo, antes de exigir a memorização, abrimos portas para que todos os alunos. Especialmente aqueles com dificuldades de aprendizagem e de memorização, encontrem sentido no que estão fazendo.
As estratégias de cálculo mental permitem que cada estudante use o raciocínio a seu favor, explore diferentes caminhos e desenvolva confiança para chegar ao resultado. A memorização virá naturalmente com o uso e a prática, mas a verdadeira base está no entendimento profundo das relações entre os números. Ensinar dessa forma é garantir que a matemática seja uma ferramenta acessível, inclusiva e significativa para todos.

