Descubra várias estratégias de cálculo mental para adição e subtração que você pode utilizar com alunos que têm dificuldades de aprendizagem na matemática.
Olá! Que bom ter você aqui!
Você já parou para pensar o quanto é difícil para um aluno que tem dificuldades de aprendizagem na matemática, conseguir compreender e usar o algoritmo tradicional?
Muitos não conseguem, se sentem incapazes de resolver problemas de adição, subtração, divisão ou multiplicação. Ficam desmotivados e pensam: “matemática não é para mim”.
Entretanto, considerando que existem diferentes formas de aprender, é muito importante apresentar aos estudantes, diferentes possibilidades de cálculo.
Isso não significa que aprender o algoritmo não seja importante.
Mas, que as estratégias de cálculo mental são muito úteis para ensinar uma matemática que o aluno não vai utilizar somente nas atividades e provas da escola, mas também e, principalmente, na vida.
Você aprendeu matemática da forma tradicional? Se sim, você provavelmente sabe que é difícil pensar em outras possibilidades de ensinar cálculos, não é mesmo?
Pois, nos ensinaram de forma convencional e conseguimos aprender. Ficamos com a impressão que devemos ensinar da mesma maneira e, também, com dificuldade em experimentar outras estratégias.
Neste post, vou apresentar várias estratégias alternativas que você pode utilizar com seus alunos, especialmente aqueles que apresentam dificuldades de aprendizagem.
Elas são importantes para que esses alunos não se sintam excluídos por não conseguirem seguir os procedimentos tradicionais. Além disso, essas estratégias podem contribuir com a compreensão do próprio algoritmo tradicional.
Acompanhe! Você irá descobrir muitas possibilidades interessantes e ter várias opções para escolher a melhor estratégia para o estilo de aprendizagem de seus alunos!
Por que é importante ensinar diferentes tipos de cálculo?
Na vida cotidiana, utilizamos diferentes formas de calcular. Às vezes usamos lápis e papel, às vezes buscamos um resultado aproximado, às vezes calculamos mentalmente e muitas vezes, utilizamos a calculadora.
Tudo depende da situação ou dos recursos que temos no momento.
Imagine se a única alternativa que você tivesse fosse resolver as operações usando o algoritmo tradicional? Tal como muitos de nós, aprendemos na escola.
E se não tiver lápis/caneta e papel, como você faria? Armar a continha no ar é tão difícil… 😅
Se você assim como eu, aprendeu a somar, subtrair, multiplicar e dividir de forma tradicional, sabe que é muito difícil calcular de outra maneira.
Mas, ao mesmo tempo que sabemos usar o algoritmo, dá um “nó” no nosso cérebro, refletir sobre o porquê do “vai um”, “pega emprestado”.
Explicar por que na divisão começamos a “continha” pela esquerda, se na adição, subtração e multiplicação iniciamos pela direita.
Por que quando estamos operando com o segundo algarismo na multiplicação, deixamos um espaço vazio à direita?…
É difícil refletir sobre os procedimentos que realizamos de forma tão automatizada, não é mesmo?
Agora, imagine para um aluno que não consegue usar esses procedimentos tradicionais para calcular.
Muitos estudantes se perdem ao tentar aplicar o algoritmo tradicional, principalmente quando não compreendem o raciocínio por trás da operação.
Quando trabalhamos com diferentes tipos de cálculo, estamos dando a oportunidade para os estudantes refletirem sobre as operações básicas e sobre o SND, experimentarem novas estratégias, trocarem ideias com os colegas sobre como resolveram os problemas.
Ao apresentar múltiplas abordagens, estimulamos:
- Flexibilidade cognitiva
- Autonomia na resolução de problemas
- Compreensão real (e não apenas memorização)
- A autoestima matemática do aluno
Enfim, eles têm mais oportunidades de aprendizado, respeitando seus ritmos e formas particularidades de aprender.
Por que é importante ensinar estratégias de cálculo mental para adição e subtração?
Primeiramente, vamos refletir sobre o conceito de cálculo mental.
Quando falamos em cálculo mental, pensamos logo em “resolver contas de cabeça” e de forma rápida.
No entanto, atualmente, as pesquisas nos mostram que na verdade, o cálculo mental não precisa ser feito apenas “de cabeça” ou de forma rápida. Ele é entendido como um cálculo “pensado”, no qual acontece uma reflexão.
Ou seja, ele não segue uma “receita de bolo”, com um passo a passo previamente estabelecido como acontece com os algoritmos.
Assim, uma mesma operação pode ser resolvida por diversos procedimentos.
Esse fato já sugere um dos motivos para ensinar cálculo mental: estimular a criatividade e a criação de estratégias pessoais para resolver problemas matemáticos.
Além disso, o cálculo mental é importante para
- desenvolver o raciocínio,
- estimular a memória,
- descobrir a relação entre as operações,
- compreender o nosso sistema de numeração decimal.
E o mais importante, mostrar que não existe uma única maneira de aprender matemática, que favorece só um grupo de pessoas. Mas, que todos nós podemos nos aventurar nesse mundo de números!
A boa notícia é que existem estratégias visuais e intuitivas que ajudam os alunos a construir o entendimento matemático com mais sentido — e mais segurança.
Vamos conhecer algumas?
Conhecimentos prévios necessários
Antes de apresentar todas as possibilidades, convém destacar que é fundamental que os estudantes saibam:
- Decompor e compor números;
- Cálculos básicos, por exemplo, para obter o número 10, podemos somar 9+1 ou 8+2, 7+3, 6+4, 5+5;
- Adições e subtrações simples, de unidades;
- Construir generalizações. Por exemplo, se 6+3=9, logo, 60+30=90 e 600+300=900
Estratégias de cálculo mental para adição
1. Decomposição
Aqui a ideia é decompor os números em centenas, dezenas, unidades. É uma estratégia útil para ajudar as crianças a entenderem o valor posicional.
Exemplo: 47+35
Passo a passo:
- Peça para o aluno decompor os números:
→ 47 = 40 + 7
→ 35 = 30 + 5 - Somar as dezenas:
→ 40 + 30 = 70 - Somar as unidades:
→ 7 + 5 = 12 - Juntar tudo:
→ 70 + 12 = 82
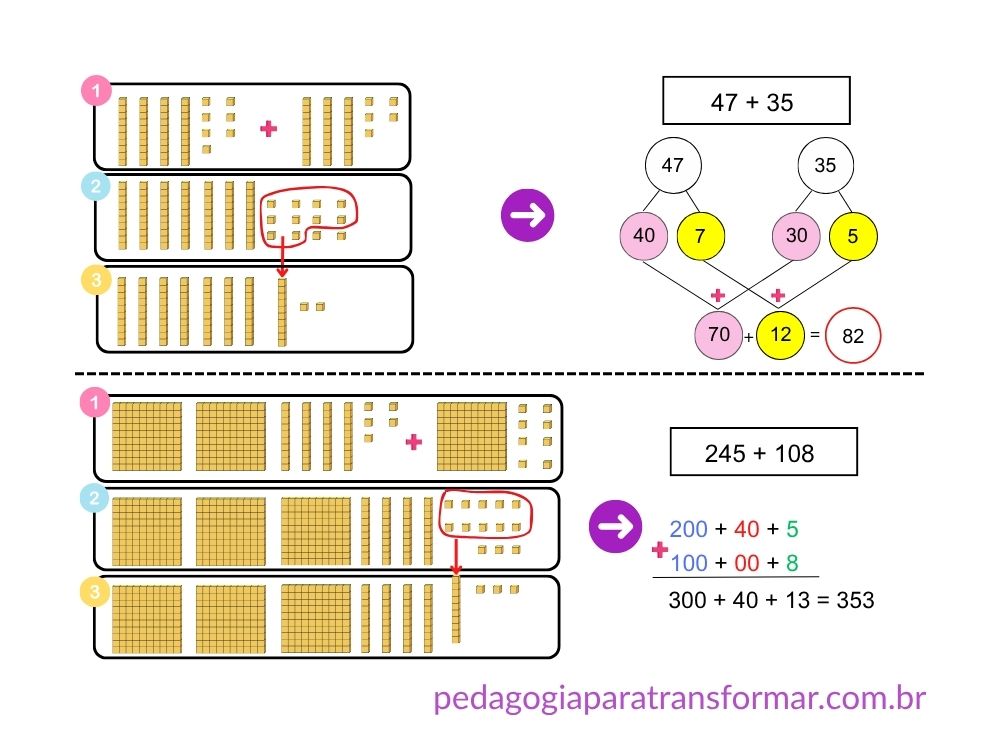
Observe que o Material Dourado facilita a visualização concreta da decomposição.
2. Reta numérica ou “pulos”
Disponibilize uma reta numérica e peça para o aluno começar com um número e ir “pulando” com somas menores.
Exemplo: 38 + 24
Passo a passo:
- Ajude o aluno a localizar o 38 na reta numérica.
- Pular +10 → 48
- Pular +10 → 58
- Pular +4 → 62
Resultado: 62
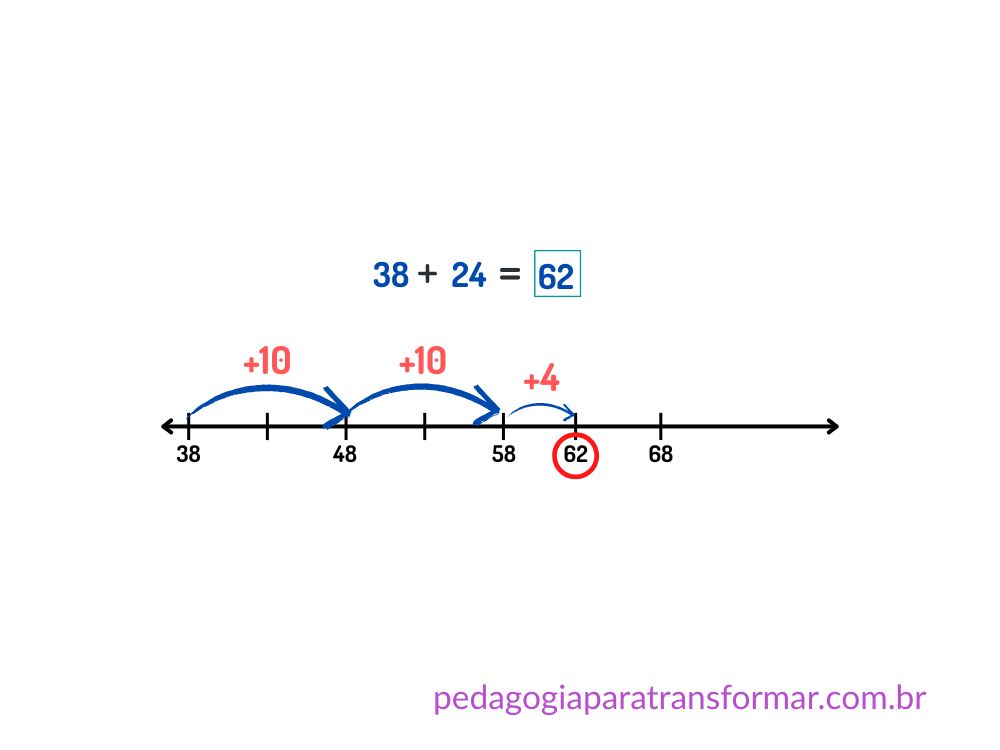
3. Compensação (Ajuste inteligente)
Para utilizar essa estratégia, o aluno precisa arredondar um número para facilitar o cálculo e depois ajustar.
Exemplo: 49 + 23
Passo a passo:
- Peça para o aluno arredondar para um número mais fácil de somar: 49 para 50.
- 50 + 23 = 73
- Como adicionou 1 a mais, peça para ele subtrair 1:
→ 73 – 1 = 72
Outro exemplo: 33 + 12
- Ensine o aluno a ajustar os números para facilitar o cálculo. Nesse caso, retirar 2 unidades do número 12, tornando-se 10.
- Em seguida, adicionar essas 2 a 33, obtendo 35.
- A nova operação (35 + 10) é mais fácil de calcular.

4. Somar em partes (por etapas)
Essa é uma estratégia boa para quem se perde com números grandes.
Exemplo: 154 + 143
Passo a passo:
Ajude o estudante a pensar em possibilidades de ir somando em partes, para trabalhar com números menores. Por exemplo, somar primeiro 100, depois o 40 e por último, o 8.
- 154 + 100 = 254
- 254 + 40 = 294
- 294 + 3 = 297

5. Somar buscando o 10
Exemplo: 8 + 6
Passo a passo:
- Incentive o aluno a completar o primeiro número para chegar ao 10.
- Que número somado ao 8 dá o resultado 10?
- Em seguida, peça para decompor o número 6, partindo do número do 2:
2 + 4
- Agora, a soma fica mais simples para a criança resolver.
8 + 2=10
10 + 4=14

6. Somar buscando o 100
Exemplo: 70 + 50
Passo a passo:
- Incentive o aluno a completar o primeiro número para chegar a 100.
- Que número somado ao 70 dá o resultado 100? 30
- Em seguida, peça para decompor o número 50, partindo do número do 30:
30 + 20
- Agora, a soma fica mais simples:
70 + 30 = 100
100 + 20 = 120
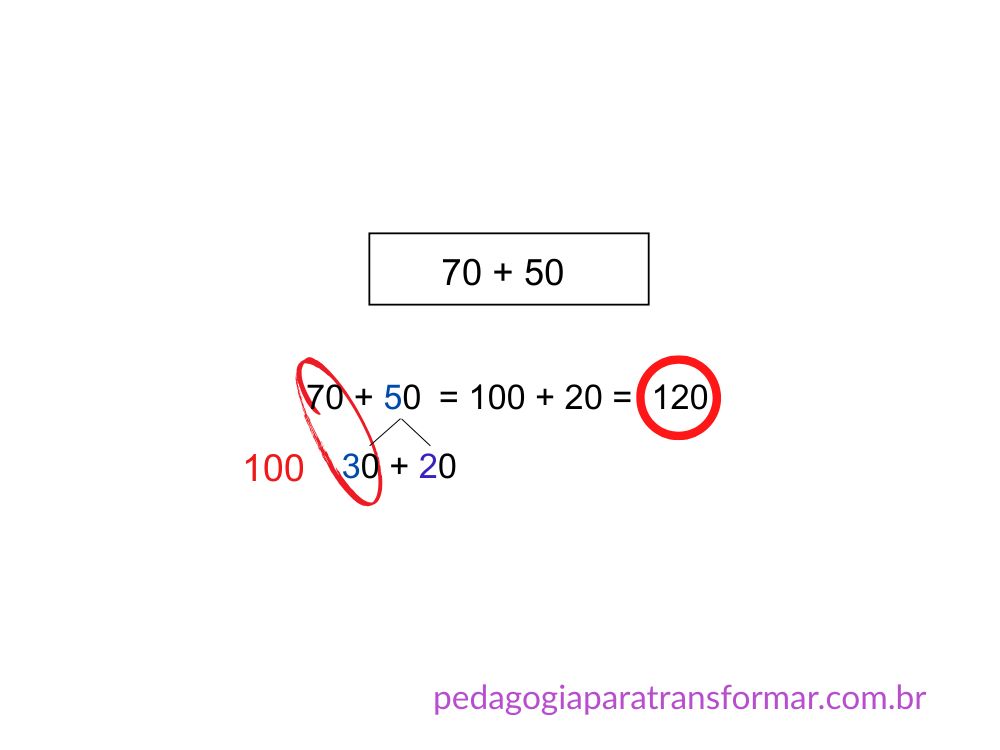
Estratégias de cálculo mental para Subtração
1. Decomposição
Exemplo: 63 – 21
Passo a passo:
- Peça para o estudante decompor os números:
→ 63 = 60 + 3
→ 21 = 20 + 1
- Em seguida, subtrair em partes:
→ 60 – 20 = 40
→ 3 – 1 = 2
→ 40 + 2 = 42
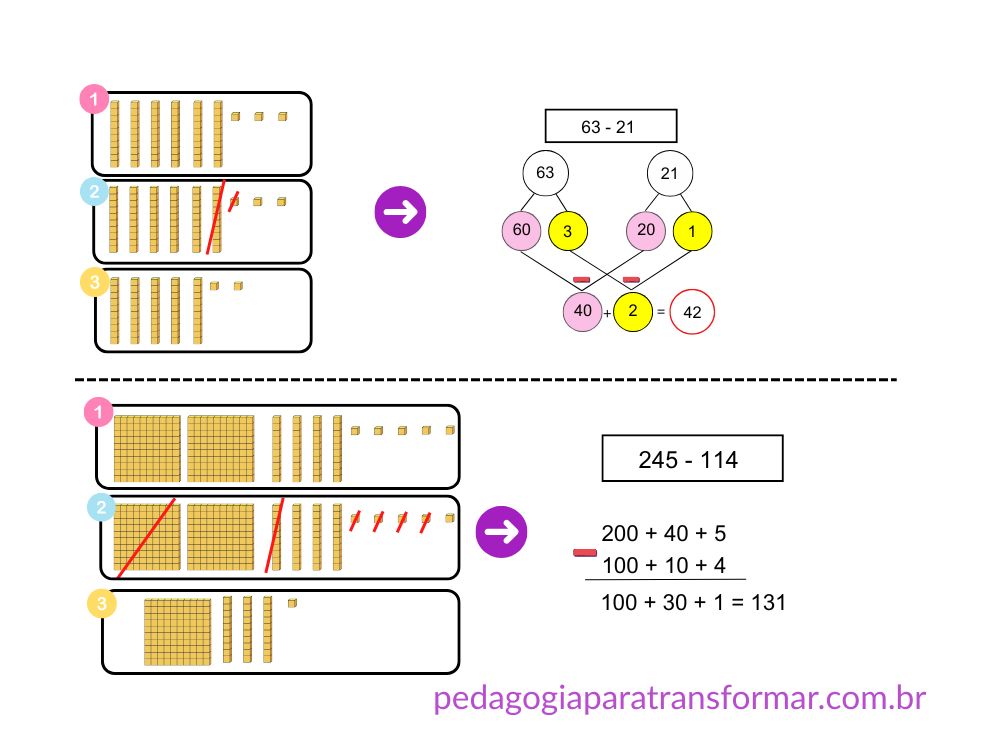
2. Contagem para cima
Em vez de tirar, nessa estratégia ajudamos o aluno a pensar quanto falta de um número ao outro. Crianças que têm dificuldade com reagrupamento adoram esse método.
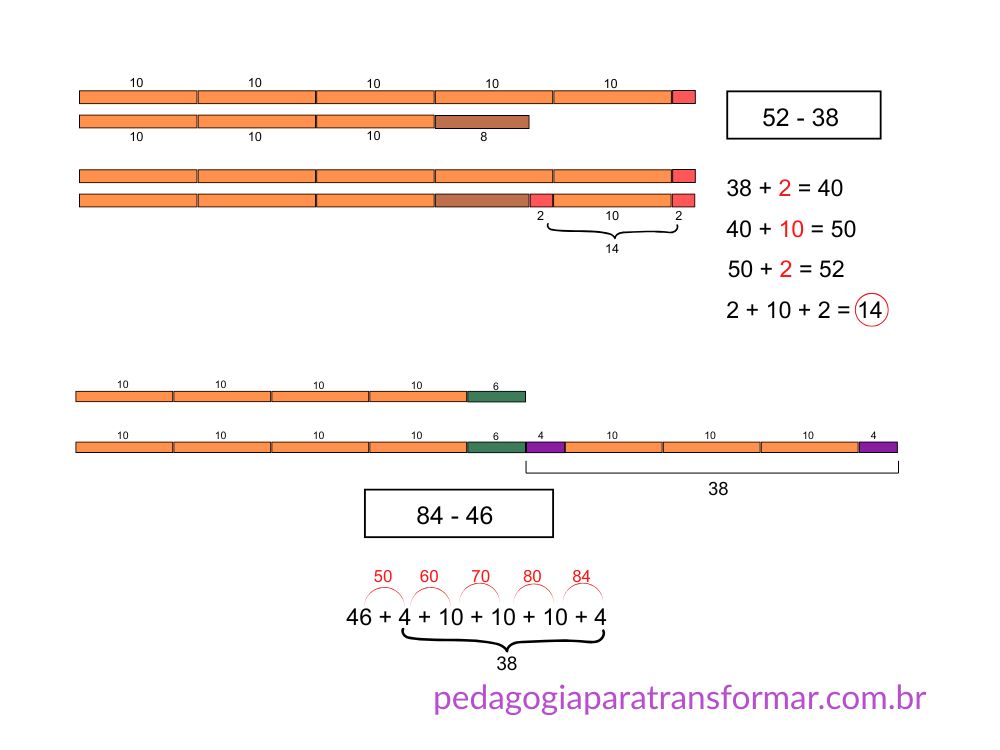
Exemplo: 52 – 38
Passo a passo:
- Questione: quanto falta de 38 até 52?
- De 38 a 40 → 2
- De 40 a 50 → 10
- De 50 a 52 → 2
- Some os passos: 2 + 10 + 2 = 14
Observe a representação com a Escala Cuisenaire. Essas barrinhas facilitam bastante a compreensão e podem ser utilizadas como apoio para o cálculo mental.
3. Compensação
Exemplo: 61 – 29
Passo a passo:
- Nessa estratégia, o objetivo é arredondar para um número mais fácil de subtrair. No exemplo, 29 para 30.
- 61 – 30 = 31
- Como tirou 1 a mais, é preciso devolver:
- 31 + 1 = 32

4. Subtrair em partes
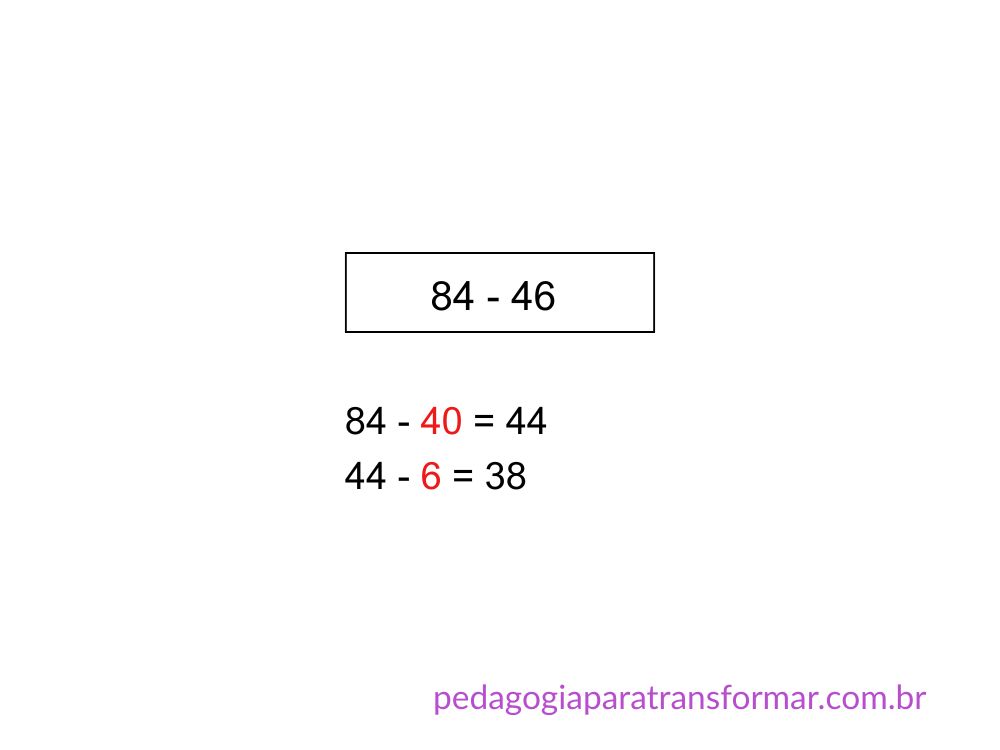
Exemplo: 84 – 46
Passo a passo:
Ajude a criança a pensar em maneiras de subtrair em partes para trabalhar com números menores. Por exemplo, subtrair 40 e depois 6.
- 84 – 40 = 44
- 44 – 6 = 38
5. Decomposição do minuendo
Decompor o minuendo em partes convenientes até conseguir “retirar” o subtraendo. É uma forma de subtração por partes.
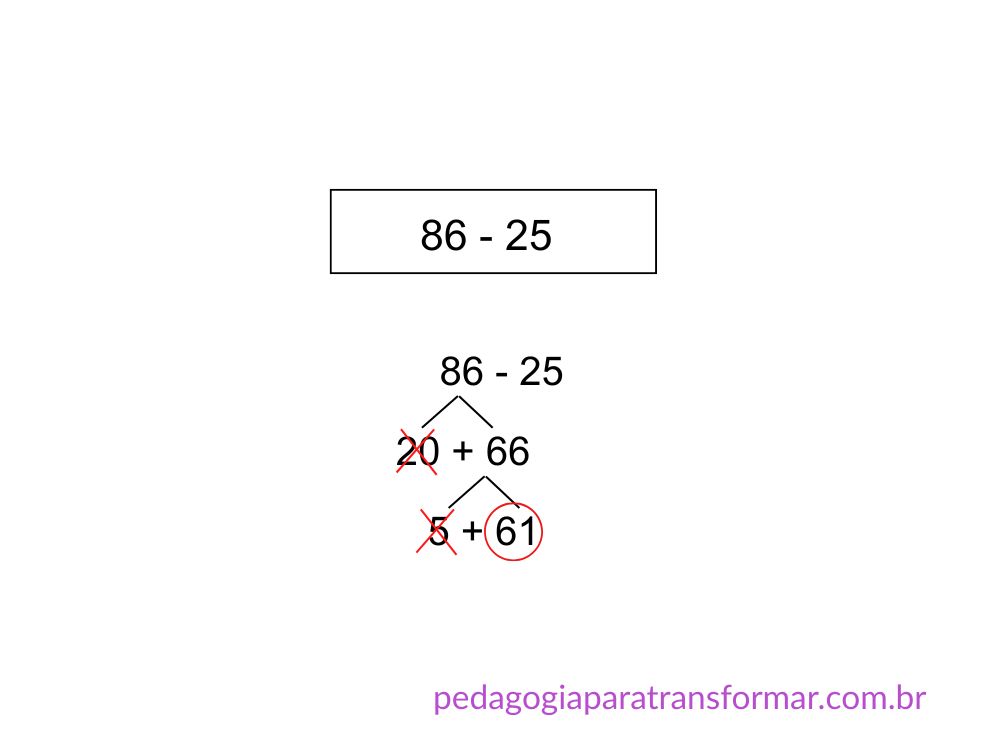
Exemplo: 86 − 25
Passo a passo:
- Peça para o aluno decompor o subtraendo: 25 = 20 + 5.
- Agora, peça para decompor o minuendo, partindo do número 20. Quanto falta de 20 para chegar a 86? 66.
- 86 = 20 + 66. Risque o 20 porque corresponde ao 20 do subtraendo.
- Agora decomponha o que sobrou (66) partindo do número 5 (pois, já tiramos o 20, agora falta 5 para 25).
- 66 = 5 + 61. Risque o 5 porque corresponde ao 5 do subtraendo.
- O que restou depois de riscar 20 e 5 é 61, o resultado final.
- Confira: 61 + 25 = 86
Conclusão
Ensinar diferentes estratégias não é “complicar”, mas sim abrir caminhos.
Cada criança que se sente capaz de resolver um problema com suas próprias ferramentas ganha confiança para continuar aprendendo.
Como educadores, nosso papel é ampliar possibilidades, especialmente para os alunos que mais precisam de acolhimento e flexibilidade na forma de aprender.
Como disse no início, não significa ensinar o cálculo mental e deixar o algoritmo de lado. Mas, trabalhar paralelamente.
No início, parece confuso, pois não estamos acostumadas (os) com uma matemática reflexiva, aberta. Mas, é uma oportunidade também para nós, termos contato com uma nova visão sobre a matemática.
Você já utiliza alguma dessas estratégias?

